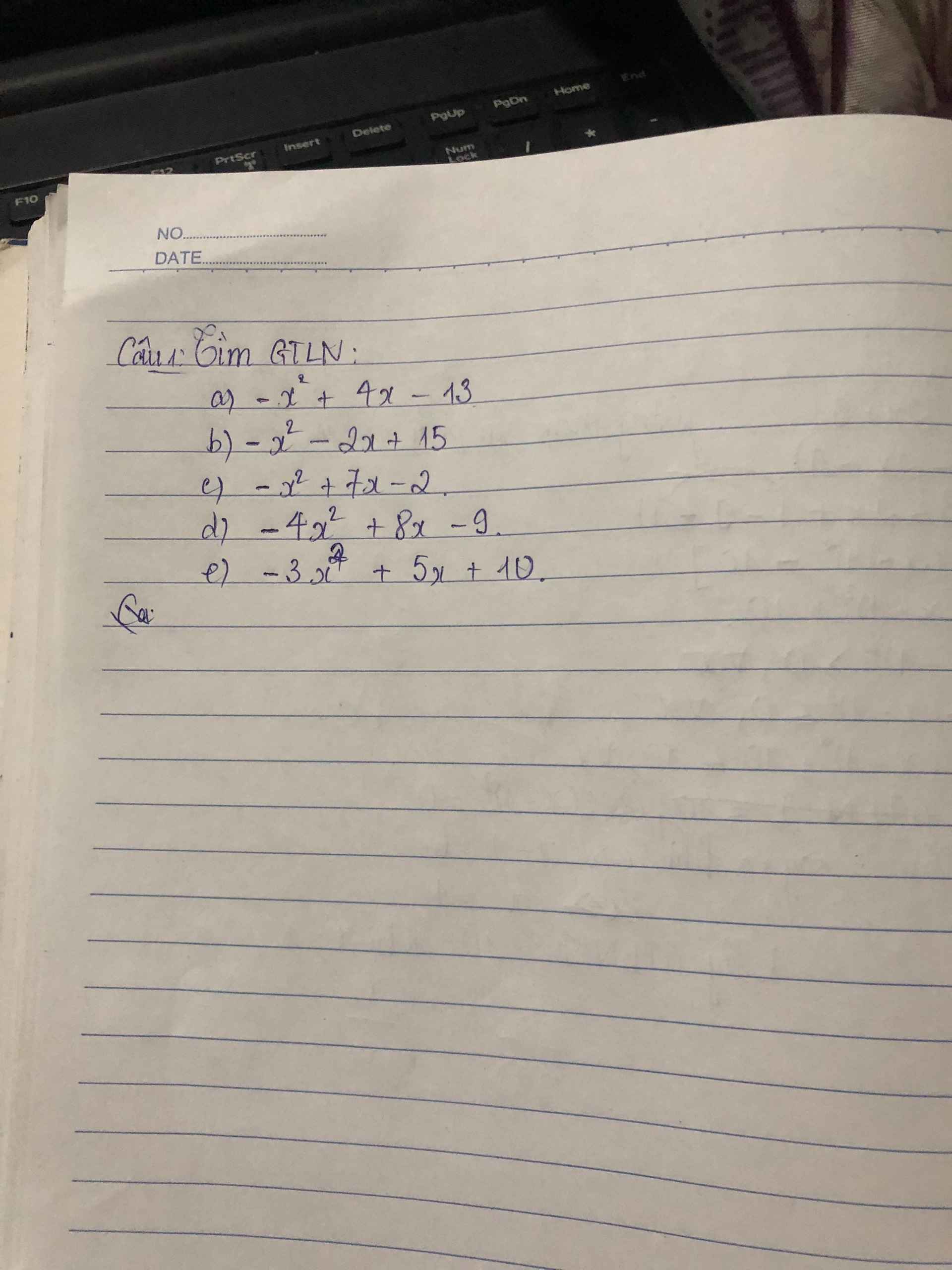Question

Answer 1

a) \(-x^2+4x-13=-x^2+4x-4-9\) \(=-\left(x^2-4x+4\right)-9\) \(=-\left[\left(x-2\right)^2+9\right]\) 

Có \(\left(x-2\right)^2\ge0\) với mọi x

 \(\Rightarrow\left(x-2\right)^2+9\ge0+9\)

 \(\Rightarrow-\left[\left(x-2\right)^2+9\right]\le9.\left(-1\right)\)

\(\Leftrightarrow-x^2+4x-13\le-9\)

Vậy giá trị lớn nhất của \(-x^2+4x-13\) là -9

 

Answer 2

b) \(-x^2-2x-15=-x^2-2x-1-14\) \(=-\left(x^2+2x+1\right)-14\) \(=-\left(x-1\right)^2-14\) 

Có \(\left(x-1\right)^2\ge0\) với mọi x

\(\Rightarrow-\left(x-1\right)^2\le0\)

\(\Rightarrow-\left(x-1\right)^2-14\le0-14\)

\(\Leftrightarrow-x^2-2x+15\le-14\)

Vậy giá trị lớn nhất của\(-x^2-2x+15\) là -14