Em hãy dựng tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh AC của tam giác.
Bài 8. Tính chất ba đường cao của tam giác
QL
Hướng dẫn giải
Thảo luận (1)
QL
Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC.
Hướng dẫn giải
Thảo luận (1)
QL
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a)
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b).
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
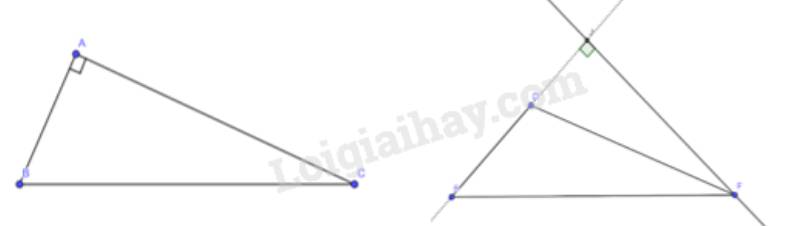
a) Ta thấy ở tam giác ABC vuông tại A thì BA chính là đường cao từ đỉnh B của tam giác vuông ABC
b) Ta thấy đường cao tam giác tù DEF xuất phát từ đỉnh F sẽ nằm ngoài tam giác DEF và chân đường cao nằm trên đoạn kéo dài của đoạn ED.
Trả lời bởi Kiều Sơn Tùng
QL
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
Hướng dẫn giải
Thảo luận (1)
QL
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
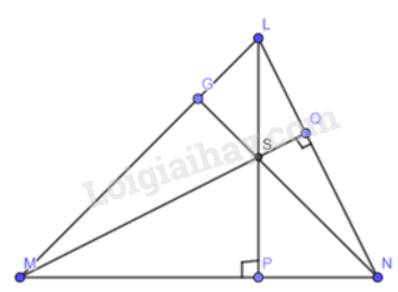
Theo giả thiết ta có : LP và MQ là 2 đường cao của tam giác
Chúng cắt nhau tại S
Theo định lí 3 đường cao trong 1 tam giác cùng đi qua 1 điểm
\( \Rightarrow \)Đường cao từ đỉnh N cũng đi qua S
\( \Rightarrow \)NS là đường cao của tam giác MNL
\( \Rightarrow \) NS vuông góc với ML tại G (là chân đường cao)
Trả lời bởi Kiều Sơn Tùng
QL
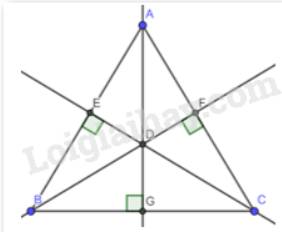
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
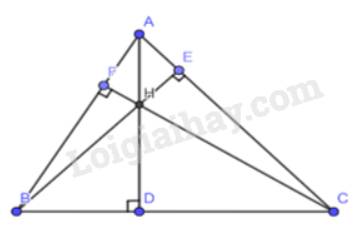
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.
Trả lời bởi Kiều Sơn Tùng
QL
Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
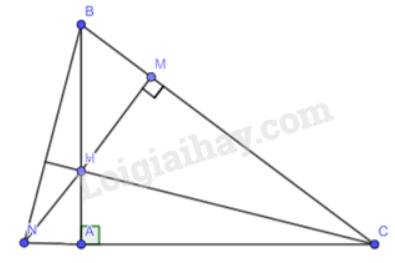
Vì tam giác ABC vuông tại A theo giả thiết nên BA vuông góc với AC
Vì HM cắt AC tại N mà HM vuông góc với BC (giả thiết)
\( \Rightarrow \) NM vuông góc với BC tại M
Xét tam giác NBC có NM và BA là 2 đường cao
Mà MN cắt AB tại H nên H là trực tâm của tam giác NBC
\( \Rightarrow \) CH đường cao của tam giác NBC (3 đường cao của tam giác đi qua 1 điểm)
\( \Rightarrow \) CH vuông góc với NB
Trả lời bởi Kiều Sơn Tùng
QL
Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
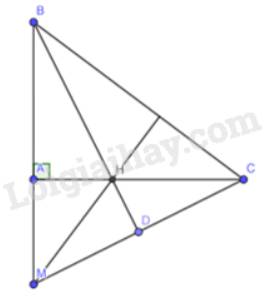
Gọi D giao điểm của tia phân giác của góc B và MC
Xét tam giác BDM và tam giác BDC có :
BD chung
\(\widehat {MBD} = \widehat {CBD}\) ( BD là phân giác của góc B)
BM = BC ( giả thiết )
( \Rightarrow \Delta BDM=\Delta BDC\)(c.g.c)
\( \Rightarrow \widehat {BDM} = \widehat {BDC}\)(2 góc tương ứng)
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {BDM} = \widehat {BDC} = {90^o} \Rightarrow BD \bot CM\)
Mà AC cắt BD tại H \( \Rightarrow \) H là trực tâm tam giác BMC
\( \Rightarrow \) MH là đường cao của tam giác BMC (định lí 3 đường cao đi qua trực tâm tam giác)
\( \Rightarrow \) MH vuông góc với BC
Trả lời bởi Kiều Sơn Tùng
QL
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC b) BE vuông góc với DC
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
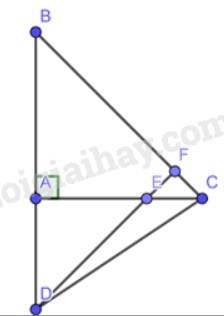
a) Vì tam giác ABC vuông cân tại A
\( \Rightarrow \) \(\widehat B = \widehat C = {45^o}\)(2 góc ở đáy bằng nhau)
Xét tam giác AED có :
AE = AD
AC vuông góc với AB
\( \Rightarrow \) Tam giác AED vuông cân tại A
\( \Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}\)
Mà \(\widehat {AED};\widehat {CEF}\)là 2 góc đối đỉnh \( \Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}\)
Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :
\( \Rightarrow \widehat F + \widehat C + \widehat E = {180^o}\)
\( \Rightarrow \widehat F = {180^o} - {45^o} - {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC\)
b) Vì DE vuông góc với BC \( \Rightarrow \) DE là đường cao của tam giác BCD
Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)
\( \Rightarrow \)BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)
\( \Rightarrow \)BE vuông góc với DC
Trả lời bởi Kiều Sơn Tùng
QL
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
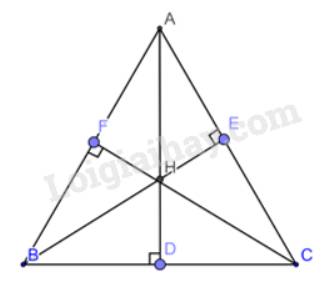
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
Trả lời bởi Kiều Sơn Tùng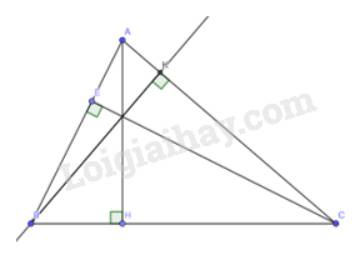
Tham khảo:
- Ta dùng êke với cạnh góc vuông đi qua đỉnh B
- Cạnh góc vuông còn lại của êke nằm trùng với AC
Trả lời bởi Kiều Sơn Tùng