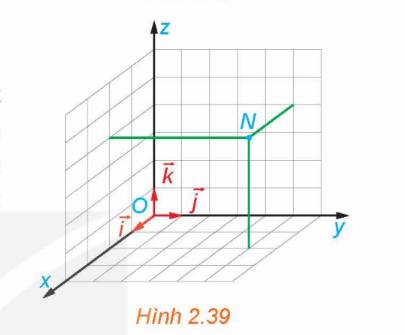
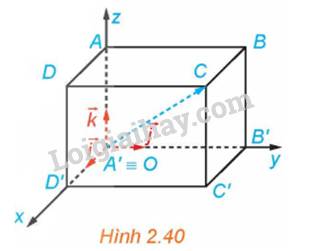
Trong không gian, xét ba trục Ox, Oy, Oz có chung gốc O và đôi một vuông góc với nhau. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) là các vectơ đơn vị trên các trục đó (H.2.35).
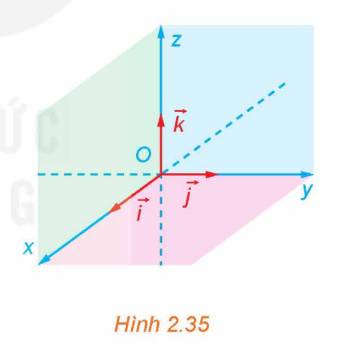
a) Gọi tên các mặt phẳng tọa độ có trong Hình 2.35.
b) Các mặt phẳng tọa độ trong Hình 2.35 có đôi một vuông góc với nhau không?

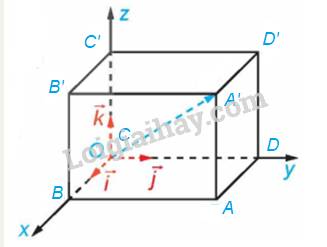
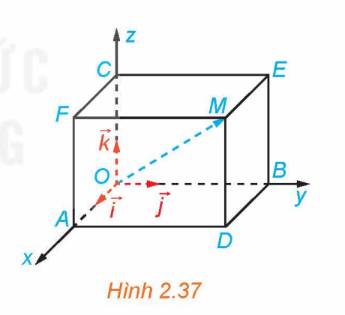

a) Các mặt phẳng có trong hình vẽ là: Mặt phẳng (Oxy), (Oyz), (Ozx).
b) Vì \(Ox \bot Oy,Oy \bot Oz\), Ox và Oz cắt nhau tại O và nằm trong mặt phẳng (Oxz) nên \(Oy \bot \left( {Oxz} \right)\). Mà \(Oy \subset \left( {Oxy} \right) \Rightarrow \left( {Oxz} \right) \bot \left( {Oxy} \right),Oy \subset \left( {Oyz} \right) \Rightarrow \left( {Oyz} \right) \bot \left( {Oxz} \right)\)
Chứng minh tương tự ta có: \(\left( {Oyz} \right) \bot \left( {Oxy} \right)\)
Vậy ba mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau.
Trả lời bởi Hà Quang Minh