So sánh hai góc ở hình 10
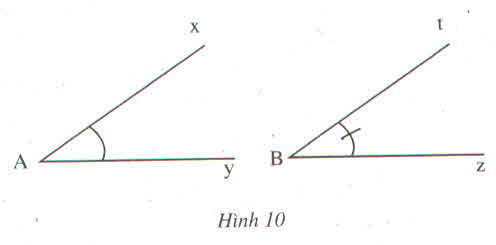
So sánh hai góc ở hình 10

Tính tổng số đo hai góc trên hình 10 ?

Trên mặt phẳng, cho tia Ax. Có thể vẽ được mấy tia Ay sao cho \(\widehat{xAy}=50^0\) ?
Vẽ góc vuông BAC
Hướng dẫn :
Cách 1 : Dùng thước đo góc
Cách 2 : Dùng êke
Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O. Biết \(\widehat{xOt}=30^0,\widehat{yOt'}=60^0\). Tính số đo các góc \(\widehat{yOt},\widehat{tOt'}\) ?
Giải:
Hai góc xOt và yOt kề bù nên:
= 1800 -
= 1800 - 300 = 1500
Hai tia Ot' và Ot cùng thuộc nửa mặt phẳng bờ Oy mà <
nên tia Ot' nằm giữa hai tia Oy và Ot, suy ra
nên tia Ot' nằm giữa hai tia Oy và Ot, suy ra : +
=
Thay số ta được: 600+ 600 = 1500
Suy ra:
= 900
Trả lời bởi Thien Tu Borum
Trên cùng một nửa mặt phẳng bờ chứa tia OA, vẽ hai tia OB, OC sao cho \(\widehat{BOA}=45^0,\widehat{COA}=55^0\). Tính số đo góc BOC ?
Giải:
Hai tia OB, OC cùng nửa mặt phẳng bờ chứa tia OA mà
<
nên tia OC nằm giữa hai tia OA,OB
suy ra +
=
hay 550 + = 1450
Vậy = 1450 - 550 = 900
Trả lời bởi Thien Tu Borum
Vẽ góc IKM có số đo bằng \(135^0\)
Vẽ góc xBy có số đo bằng \(45^0\)
Hướng dẫn : Vẽ tia Bx, sau đó trên một nửa mặt phẳng có bờ chứa tia Bx vẽ tia By sao cho \(\widehat{xBy}=45^0\)
Vẽ góc cho biết một cạnh và số đo góc đó trong bốn trường hợp sau :
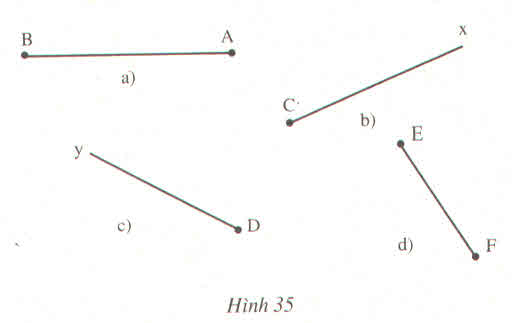
a) \(\widehat{BAC}=20^0\)
b) \(\widehat{xXz}=110^0\)
c) \(\widehat{yDx}=80^0\)
d) \(\widehat{EFy}=145^0\)
Giải:
Có thể vẽ hình như sau:
a) Đỉnh của góc là A, một cạnh là AB, cần vẽ tia AC.
b) Đỉnh của góc là C, một cạnh là Cx, cần vẽ tia Cz.
c) Đỉnh của góc là D, một cạnh là Dy, cần vẽ tia Dx.
d) Đỉnh của góc là F, Một cạnh là EF, cần vẽ tia Fy.
Trả lời bởi Thien Tu Borum
Vẽ góc xOl có số đo bằng \(40^0\) ?
Cách 1 : Đo riêng từng góc rồi so sánh hai số đo
Cách 2 : Vẽ lại 2 góc lên giấy trong . Đặt chồng hai góc sao cho đỉnh trùng nhau ,một cạnh trùng nhau ,hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi kết luận
=> Qua 2 cách trên ,ta thấy hai góc ở hình 10 có số đo bằng nhau
Trả lời bởi Mai Hà Chi