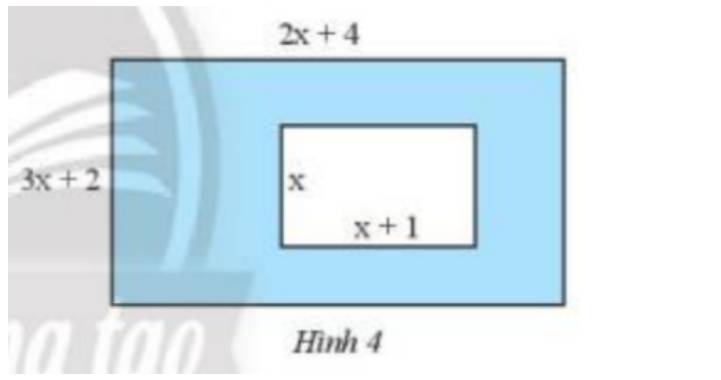
Cho hai hình chữ nhật như Hình 4. Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.
Cho hai hình chữ nhật như Hình 4. Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.

Thực hiện phép chia.
a) \((8{x^6} - 4{x^5} + 12{x^4} - 20{x^3}):4{x^3}\)
b) \((2{x^2} - 5x + 3):(2x - 3)\)
Tham khảo:
a) \((8{x^6} - 4{x^5} + 12{x^4} - 20{x^3}):4{x^3}\)
\( = (8{x^6}:4{x^3}) - (4{x^5}:4{x^3}) + (12{x^4}:4{x^3}) - (20{x^3}:4{x^3})\)
\( = 2{x^2} - {x^2} + 3x - 5\)
b)

Vậy \((2{x^2} - 5x + 3):(2x - 3)= x - 1\)
Trả lời bởi Kiều Sơn TùngThực hiện phép chia.
a) \((4{x^2} - 5):(x - 2)\)
b) \((3{x^3} - 7x + 2):(2{x^2} - 3)\)
Tham khảo:
a) \((4{x^2} - 5):(x - 2) = \dfrac{{4{x^2} - 5}}{{x - 2}} = 4x + 8 + \dfrac{{11}}{{x - 2}}\)
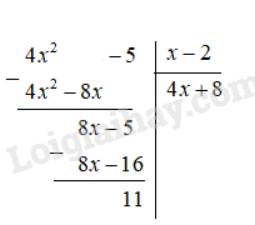
Vậy \( (4{x^2} - 5):(x - 2)= 4x + 8 + \dfrac{{11}}{{x - 2}}\)
b) \((3{x^3} - 7x + 2):(2{x^2} - 3) = \dfrac{{3{x^3} - 7x + 2}}{{2{x^2} - 3}}\)

Vậy \( (3{x^3} - 7x + 2):(2{x^2} - 3)= \dfrac{3}{2}x + \dfrac{{\dfrac{-5}{2}x + 2}}{{2{x^2} - 3}}\)
Trả lời bởi Kiều Sơn TùngTính chiều dài của một hình chữ nhật có diện tích bằng \((4{y^2} + 4y - 3)\)\(c{m^2}\) và chiều rộng bằng (2y – 1) cm.
Tham khảo:
Diện tích hình chữ nhật = chiều dài . chiều rộng
\( \Rightarrow (4{y^2} + 4y - 3):(2y - 1) = \dfrac{{4{y^2} + 4y - 3}}{{2y - 1}}\)
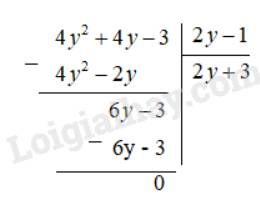
Vậy chiều dài hình chữ nhật là : 2y + 3 cm
Trả lời bởi Kiều Sơn TùngCho hình hộp chữ nhật có thể tích bằng (\(3{x^3} + 8{x^2} - 45x - 50\)) \(c{m^3}\), chiều dài bằng (x + 5) cm và chiều cao bằng (x + 1) cm. Hãy tính chiều rộng của hình hộp chữ nhật đó.
Tham khảo:
Ta có thể tích hình hộp chữ nhật bằng tích chiều cao và diện tích đáy
Nên chiều rộng của hình chữ nhật = thể tích : ( chiều cao . chiều dài )
Diện tích đáy là \((x + 5)(x + 1) = {x^2} + 6x + 5\)
Thay các số ở đề bài cho vào công thức trên ta được :
\( = \dfrac{{3{x^3} + 8{x^2} - 45x - 50}}{{(x + 5)(x + 1) = {x^2} + 6x + 5}} = \dfrac{{3{x^3} + 8{x^2} - 45x - 50}}{{{x^2} + 6x + 5}}\)

Vậy chiều dài hình hộp chữ nhật là 3x – 10 cm
Trả lời bởi Kiều Sơn Tùng
Ta có diện tích hình chữ nhật lớn là : \((2x + 4)(3x + 2) = 2x(3x + 2) + 4(3x + 2) = 6{x^2} + 4x + 12x + 8 = 6{x^2} + 16x + 8\)
Diện tích hình chữ nhật nhỏ là : \(x(x + 1) = {x^2} + x\)
Diện tích phần cần tìm là : \(6{x^2} + 16x + 8 - {x^2} - x\)\( = 5{x^2} + 15x + 8\)
Trả lời bởi Hà Quang Minh