Cho \(E = \{ x \in \mathbb{N}|x < 10\} ,A = \{ x \in E|x\)là bội của 3\(\} ,\)\(B = \{ x \in E|x\) là ước của 6\(\} .\)
Xác định các tập hợp \(A\backslash B,{\rm{ }}B\backslash A,\;{C_E}A,\;{C_E}B,{C_E}(A \cup B),{C_E}(A \cap B).\)
Cho \(E = \{ x \in \mathbb{N}|x < 10\} ,A = \{ x \in E|x\)là bội của 3\(\} ,\)\(B = \{ x \in E|x\) là ước của 6\(\} .\)
Xác định các tập hợp \(A\backslash B,{\rm{ }}B\backslash A,\;{C_E}A,\;{C_E}B,{C_E}(A \cup B),{C_E}(A \cap B).\)
Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
a) A và \(A \cup B\)
b) A và \(A \cap B\)
Trong số 35 học sinh của lớp 10H, có 20 học sinh thích môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:
a) Có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
b) Có bao nhiêu học sinh không thích cả hai môn này?
Gọi A, B lần lượt là tập hợp các học sinh thích môn Toán và Tiếng Anh, X là tập hợp học sinh lớp 10H.
Theo giả thiết, \(n(A) = 20,n(B) = 16,n(A \cap B) = 12,n(X) = 35\)

a) Nhận thấy rằng, nếu tính tổng \(n(A) + n(B)\) thì ta được số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, nhưng số học sinh thích cả hai môn Toán và Tiếng Anh được tính hai lần. Do đó, số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 20 + 16 - 12 = 24\)
b) Trong số 35 học sinh lớp 10H, có 24 học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, còn lại số học sinh không thích cả hai môn này là: \(35 - 24 = 11\) (học sinh).
Trả lời bởi Hà Quang MinhXác định các tập hợp sau đây:
a) \(( - \infty ;0] \cup [ - \pi ;\pi ]\)
b) \([ - 3,5;2] \cap ( - 2;3,5)\)
c) \(( - \infty ;\sqrt 2 ] \cap [1; + \infty )\)
d) \(( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\)
Tham khảo:
a) Để xác định tập hợp \(A = ( - \infty ;0] \cup [ - \pi ;\pi ]\), ta vẽ sơ đồ sau đây:
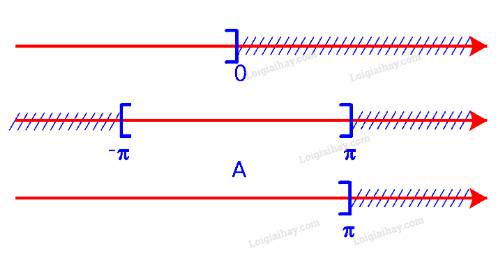
Từ sơ đồ, ta thấy \(A = ( - \infty ;\pi ]\)
b) Để xác định tập hợp \(B = [ - 3,5;2] \cap ( - 2;3,5)\), ta vẽ sơ đồ sau đây:
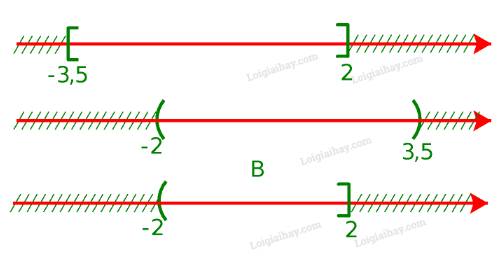
Từ sơ đồ, ta thấy \(B = ( - 2;2]\)
c) Để xác định tập hợp \(C = ( - \infty ;\sqrt 2 ] \cap [1; + \infty )\), ta vẽ sơ đồ sau đây:
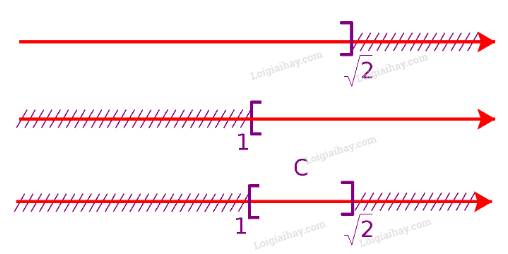
Từ sơ đồ, ta thấy \(C = [1;\sqrt 2 ]\)
d) Để xác định tập hợp \(D = ( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\), ta vẽ sơ đồ sau đây:
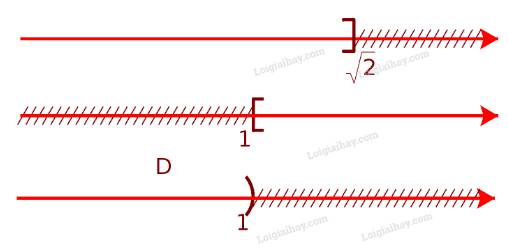
Từ sơ đồ, ta thấy \(D = ( - \infty ;1)\)
Trả lời bởi Kiều Sơn Tùng
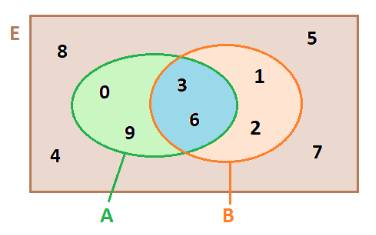
\(E = \{ x \in \mathbb{N}|x < 10\} = \{ 0;1;2;3;4;5;6;7;8;9\} \)
\(A = \{ x \in E|x\) là bội của 3\(\} \)\( = \{ 0;3;6;9\} \)
\(B = \{ x \in E|x\) là ước của 6\(\} \)\( = \{1;2;3;6\} \)
Ta có: \(A\backslash B = \left\{ {0;9} \right\}\), \(B\backslash A = \left\{ {1;2} \right\}\)
\({C_E}A = \{ 1;2;4;5;7;8\} ,\;{C_E}B = \{ 0;4;5;7;8;9\} \)
\(A \cap B = \{ 3;6\} \Rightarrow {C_E}(A \cap B) = {C_E}B = \{0;1;2;4;5;7;8;9\} \)
\(A \cup B = \{ 0;1;2;3;6;9\} \Rightarrow {C_E}(A \cup B) = {C_E}A = \{ 4;5;7;8\} \)
Trả lời bởi Hà Quang Minh