Một tổ trong lớp 11A có 10 học sinh. Điểm kiểm tra học kì I của 10 bạn này ở hai môn Toán và Ngữ văn được cho như sau:
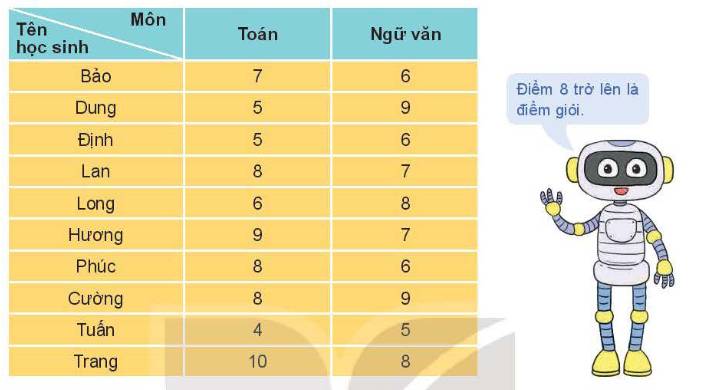
Chọn ngẫu nhiên một học sinh trong tổ. Xét các biến cố sau:
A: “Học sinh đó được điểm giỏi môn Ngữ văn”;
B: “Học sinh đó được điểm giỏi môn Toán”;
C: “Học sinh đó được điểm giỏi môn Ngữ văn hoặc điểm giỏi môn Toán”.
a) Mô tả không gian mẫu và các tập con A, B, C của không gian mẫu.
b) Tìm \(A \cup B\)
a) A = {Dung, Long, Cường, Trang}
B = {Lan, Hương, Phúc, Cường, Trang}
C = {Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b) A ∪ B = {Dung, Long, Cường, Trang, Lan, Hương, Phúc}
Trả lời bởi Quoc Tran Anh Le