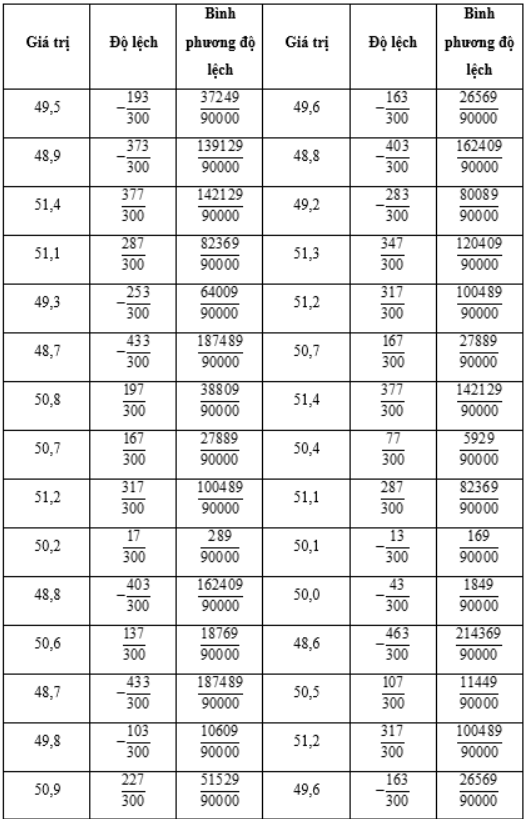
Để xác định độ ổn định của một máy đo độ ẩm không khí, người ta dùng máy này để đo 20 lần. Nếu độ lệch chuẩn của mẫu số liệu đo lớn hơn 0,15 thì người ta sẽ đưa máy đo đi sửa chữa. Trong một lần lấy mẫu, kĩ thuật viên có được mẫu số liệu ghép nhóm như sau:

Liệu có cần đưa máy đo này đi sửa chữa hay không?