Các mũi tên chỉ đường trong khu tham quan vườn thú (Hình 1) gợi nên hình ảnh các vectơ trong không gian.

Vectơ trong không gian là gì? Các phép toán về vectơ trong không gian được thực hiện như thế nào?
Các mũi tên chỉ đường trong khu tham quan vườn thú (Hình 1) gợi nên hình ảnh các vectơ trong không gian.

Vectơ trong không gian là gì? Các phép toán về vectơ trong không gian được thực hiện như thế nào?
Trong mặt phẳng, hãy nêu định nghĩa:
a) Vectơ, giá và độ dài của vectơ, hai vectơ cùng phương, hai vectơ cùng hướng;
b) Vectơ-không;
c) Hai vectơ bằng nhau, hai vectơ đối nhau.
a,
- Vecto là một đoạn thẳng có hướng
- Giá của vecto là đường thẳng chứa vecto đó
- Độ dài của vecto là khoảng cách của hai diểm đầu và cuối của vecto
- Hai vecto cùng phương là hai vecto mà giá của chúng song song hoặc trùng nhau.
- Hai vecto cùng hướng là hai vecto cùng phương nhưng có hướng khác nhau.
b, Vecto - không là vecto có điểm đầu và điểm cuối trùng nhau
c,
- 2 vectơ bằng nhau là 2 vectơ cùng hướng (cùng phương, cùng chiều) và độ lớn bằng nhau
- 2 vectơ đối nhau là 2 vectơ ngược hướng (cùng phương , ngược chiều) và độ lớn bằng nhau
Trả lời bởi datcoderCho hình hộp ABCD.A'B'C'D'. Hãy chỉ ra ba vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho mỗi vectơ đó:
a) Bằng vectơ \(\overrightarrow{AA'}\);
b) Là vectơ đối của \(\overrightarrow{AA'}\) .

a) Do các vectơ $\overrightarrow{B B^{\prime}}, \overrightarrow{C C^{\prime}}, \overrightarrow{D D^{\prime}}$ cùng hướng với vectơ $\overrightarrow{A A^{\prime}}$ và $\mathrm{AA}^{\prime}=\mathrm{BB}^{\prime}=\mathrm{CC}^{\prime}=$ $\mathrm{DD}^{\prime}$ (tính chất hình hộp) nên $\overrightarrow{\mathrm{AA}^{\prime}}=\overrightarrow{\mathrm{BB}^{\prime}}=\overrightarrow{\mathrm{CC}^{\prime}}=\overrightarrow{\mathrm{DD}^{\prime}}$. Vậy ba vectơ $\overrightarrow{B B^{\prime}}, \overrightarrow{C C^{\prime}}, \overrightarrow{D D^{\prime}}$ có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vectơ $\overrightarrow{A A^{\prime}}$.
b) Do các vectơ $\overrightarrow{B^{\prime} B}, \overrightarrow{C^{\prime} C}, \overrightarrow{D^{\prime} D}$ ngược hướng với vectơ $\overrightarrow{A A^{\prime}}$ và $\mathrm{AA}^{\prime}=\mathrm{BB}^{\prime}=\mathrm{CC}^{\prime}$ $=D^{\prime}$ (tính chất hình hộp) nên ba vectơ $\overrightarrow{B^{\prime} B}, \overrightarrow{C^{\prime} C}, \overrightarrow{D^{\prime} D}$ là ba vectơ đối của vectơ $\overrightarrow{A A^{\prime}}$
Trong không gian, cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) . Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{BC}=\overrightarrow{b}.\)
b) Tổng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) bằng vectơ nào trong Hình 4?
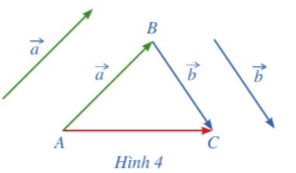
a)
– Qua A vẽ một đường thẳng song song với \(\vec a\). Trên đường thẳng đó lấy điểm B sao cho \(AB = \left| {\vec a} \right|\) và \(\overrightarrow {AB}\) cùng hướng với \({\vec a}\).
– Qua B vẽ một đường thẳng song song với \(\vec b\). Trên đườ ng thẳng đó lấy điểm C sao cho \(BC = \left| {\vec b} \right|\) và \(\overrightarrow {BC}\) cùng hướng với \({\vec b}\).
b) Ta có: \(\vec a + \vec b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Trả lời bởi datcoderCho tứ diện ABCD. Chứng minh rằng:
\(\overrightarrow{AC}+\overrightarrow{DB}=\overrightarrow{AB}+\overrightarrow{DC}.\)
Cho hình hộp ABCD.A'B'C'D' (Hình 6).
Tìm liên hệ giữa: \(\overrightarrow{AB}+\overrightarrow{AD}\) và \(\overrightarrow{AC}\); \(\overrightarrow{AC}+\overrightarrow{AA'}\) và \(\overrightarrow{AC'}\).
Từ đó, hãy suy ra rằng
\(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\)

Áp dụng quy tắc ba điểm ta thấy:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \) (1)
Mà từ hình vẽ ta thấy \(\overrightarrow {BD} = \overrightarrow {AC} \;\;\;\;\;\;\;\;\left( 2 \right)\)
Từ (1) (2) => \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {A'C} \) (3)
Mà \(\overrightarrow {A'C} = \overrightarrow {AC'} \) (4)
Từ (3), (4) suy ra \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Trả lời bởi datcoderCho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:
\(\overrightarrow{B'B}+\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{B'D}\)
Trong không gian, cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\).
Lấy một điểm M tùy ý.
a) Vẽ \(\overrightarrow{MA}=\overrightarrow{a},\overrightarrow{MB}=\overrightarrow{b},\overrightarrow{MC}=-\overrightarrow{b}.\)
b) Tổng của hai vectơ \(\overrightarrow{a}\) và \(-\overrightarrow{b}\) bằng vectơ nào trong Hình 7?

Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:
\(\overrightarrow{BB'}-\overrightarrow{C'B'}-\overrightarrow{D'C'}=\overrightarrow{BD'}.\)
\( \vec{a}\) + (\( - \vec{b}) =\) \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \) (quy tắc hình bình hành).
Trả lời bởi datcoderNêu định nghĩa tích của một số thực k ≠ 0 và vectơ \(\overrightarrow{a}\ne\overrightarrow{0}\) trong mặt phẳng.
Cho số thực \(k \ne 0\) và \(vecto\;\vec a \ne \vec 0\). Tích của số k với vecto \(\vec a\) là một vecto, kí hiệu là \(k\vec a,\;\)được xác định như sau:
- Cùng hướng với vecto \(\vec a\) nếu k > 0, ngược hướng với vecto \(\vec a\) nếu k < 0.
- Có độ dài bằng \(\left| k \right|.\left| {\vec a} \right|\).
Trả lời bởi datcoder
Sau bài học này, ta trả lời được câu hỏi trên như sau:
Trả lời bởi datcoderVectơ trong không gian là một đoạn thẳng có hướng.
Các phép toán về vectơ trong không gian:
- Tổng và hiệu của hai vectơ trong không gian
+ Quy tắc ba điểm: $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}$.
+ Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{AC}}$.
+ Quy tắc hình hộp: Nếu $A B C D \cdot A^{\prime} C^{\prime} D^{\prime}$ là hình hộp thì $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AA}^{\prime}}=\overrightarrow{\mathrm{AC}^{\prime}}$
+ Quy tắc hiệu: $\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{BA}}$.
- Tích của một số với một vectơ trong không gian: ...
- Tích vô hướng của hai vectơ trong không gian: ...