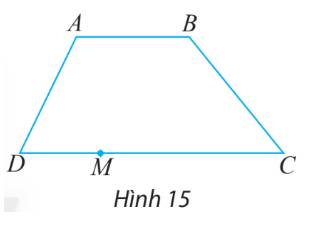
Cho hình thang ABCD có hai cạnh đáy là AB và DC (hình 15). Điểm M nằm trên đoạn DC.
a) Gọi tên các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \)
b) Gọi tên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)
Cho hình thang ABCD có hai cạnh đáy là AB và DC (hình 15). Điểm M nằm trên đoạn DC.
a) Gọi tên các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \)
b) Gọi tên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)

Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\)
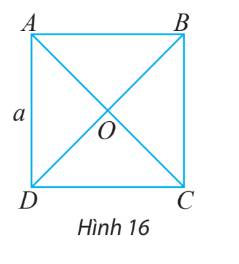
a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).
Trả lời bởi Hà Quang MinhCho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \)
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
Trả lời bởi Hà Quang MinhHãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong hình 17.
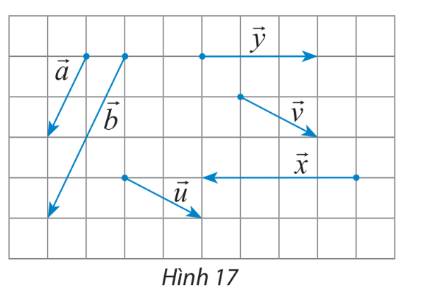
+ Các cặp vectơ cùng hướng là: \(\overrightarrow a \) và \(\overrightarrow b \); \(\overrightarrow u \) và \(\overrightarrow v \)
+ Các cặp vectơ ngược hướng là: \(\overrightarrow x \) và \(\overrightarrow y \)
+ Các cặp vectơ bằng nhau là: \(\overrightarrow u \) và \(\overrightarrow v \)
Trả lời bởi Hà Quang MinhGọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
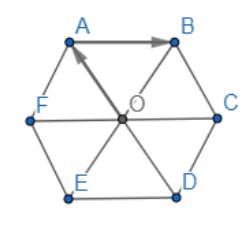
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)
b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)
Trả lời bởi Hà Quang MinhTìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong hình 18.
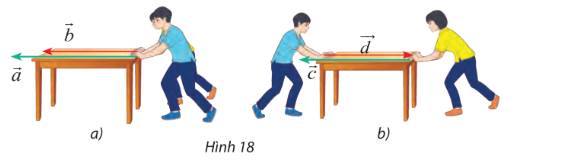
Nhận xét: giá của 4 lực đều song song hoặc trùng nhau, do đó 4 vecto là cùng phương.
Vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) có chiều từ phải sang trái còn vectơ \(\overrightarrow d \) có chiều từ trái sang phải
Vậy các vectơ (hay lực) cùng hướng với nhau là vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \).
Các vectơ (lực) \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ngược hướng với vectơ \(\overrightarrow d \).
Trả lời bởi Hà Quang Minh
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)
Trả lời bởi Hà Quang Minh