Trong Hình 1, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc trong không gian. Trong không gian, thế nào là hai đường thẳng vuông góc với nhau?

Trong Hình 1, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc trong không gian. Trong không gian, thế nào là hai đường thẳng vuông góc với nhau?

Trong mặt phẳng cho hai đường thẳng a, b.
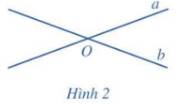
a) Nếu a và b cắt nhau tại O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?
b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?
c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
a) Nếu a và b cắt nhau tại O thì: \(0^\circ \le \left( {a,b} \right) \le 90^\circ \)
b) Nếu a // b thì không có góc tạo bởi a và b
c) Nếu a và b trùng nhau thì góc giữa a và b bằng \(0^\circ \)
Trả lời bởi Hà Quang MinhCho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam giác MNP đều. Tính góc giữa hai đường thẳng AC và BD.
Xét \(\Delta ACB\)có:
N là trung điểm BC
M là trung điểm AB
=> MN là đường trung bình của tam giác ABC
=> MN // AC
Xét tam giác ABD có:
P là trung điểm AD
M là trung điểm AB
=> MP là đường trung bình của tam giác ABD
=> MP // BD
Ta có \(\left( {AC;BD} \right) = \left( {MN;MP} \right) = \widehat {NMP} = 60^\circ \)
Trả lời bởi Quoc Tran Anh LeTrong Hình 1 ở phần mở đầu, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc. Góc giữa a và b bằng bao nhiêu độ?
Góc giữa a và b bằng \(90^o\).
Trả lời bởi Mai Trung Hải PhongCho hình lăng trụ ABC.A’B’C’ có H là trực tâm của tam giác ABC. Chứng minh rằng AH vuông góc với B’C’
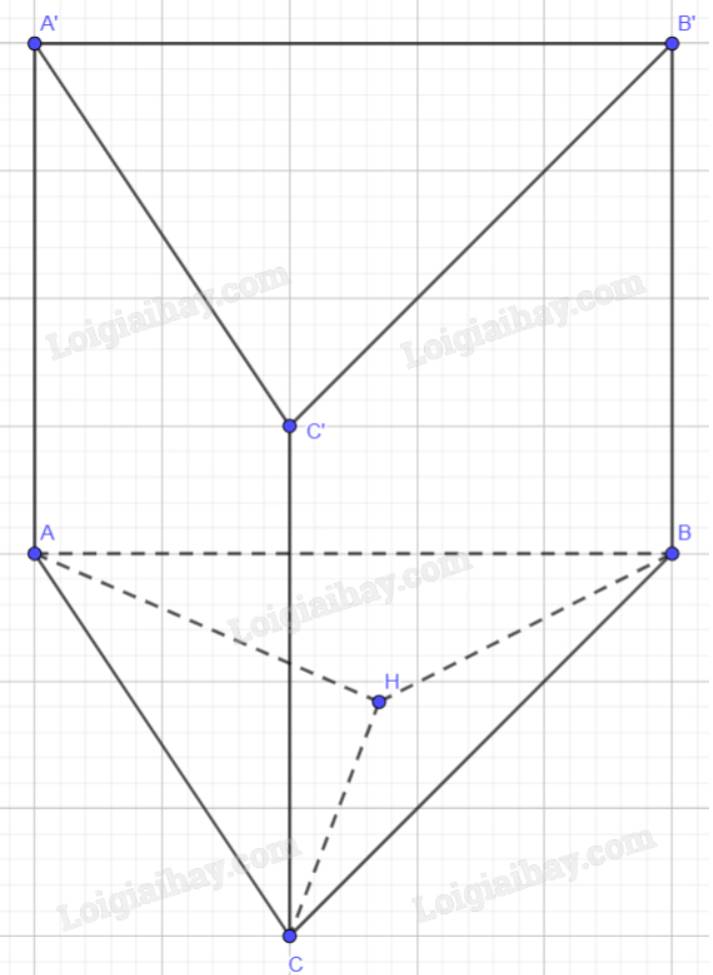
Ta có:
+ BB’ vuông góc với (ABC)
+ AH thuộc (ABC)
=> AH vuông góc với BB’
+ CC’ vuông góc (ABC)
+ AH thuộc (ABC)
=> AH vuông góc với CC’
Xét (BB’C’C) có:
+ AH vuông góc với BB’
+ AH vuông góc với CC’
=> AH vuông góc với (BB’C’C)
Mà B’C’ thuộc (BB’C’C)
=> AH vuông góc với B’C’
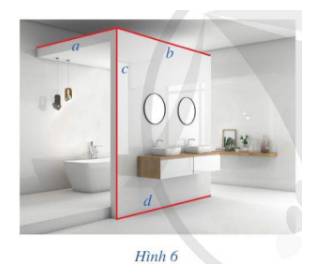
Trả lời bởi Quoc Tran Anh LeHình 6 gợi nên hình ảnh 5 cặp đường thẳng vuông góc. Hãy chỉ ra 5 cặp đường thẳng đó:
Trong Hình 7 cho ABB’A’, BCC’B’, ACC’A’ là các hình chữ nhật. Chứng minh rằng \(AB \bot CC',\,\,\,AA' \bot BC\)
- Chứng minh \(AB \bot CC'\)
+ Do ABB’A’ là hình chữ nhật \( \Rightarrow AB \bot BB'\) (1)
+ Do BCC’B’ là hình chữ nhật \( \Rightarrow BB' //CC'\) (2)
Từ (1) và (2) \( \Rightarrow AB \bot CC'\) (đpcm)
Chứng minh tương tự:
+ Do BCC’B’ là hình chữ nhật \( \Rightarrow BC \bot CC'\)
+ Do AA'C'C là hình chữ nhật \( \Rightarrow AA' //CC'\)
Từ đó \( \Rightarrow AA' \bot BC\) (đpcm)
Trả lời bởi Quoc Tran Anh LeCho hình chóp S.ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = 100^\circ \) (Hình 8) . Tính góc giữa hai đường thẳng:
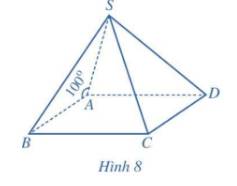
a) SA và AB
b) SA và CD
a) \(\left( {SA,AB} \right) = \widehat {SAB} = 100^\circ \)
b) Do ABCD là hình bình hành => AB // CD
\(\left( {SA,CD} \right) = \left( {SA,AB} \right) =\widehat {SAB} = 100^\circ \)
Trả lời bởi Quoc Tran Anh LeBạn Hoa nói rằng: “Nếu hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c thì a và b vuông góc với nhau”. Bạn Hoa nói đúng hay sai? Vì sao?
Bạn Hoa nói sai. Vì
+ TH1: a, b, c cùng nằm trong một mặt phẳng.
Theo quan hệ từ vuông góc tới song song: \(\left\{ \begin{array}{l}a \bot c\\b \bot c\end{array} \right. \Rightarrow a//b\)
+ TH2: a, b, c nằm khác mặt phẳng. Nếu a và b cùng vuông góc với c thì a, b nằm chéo nhau
Trả lời bởi Hà Quang Minh
tham khảo
Trong không gian, hai đường thẳng vuông góc với nhau là hai đường thẳng nằm trong hai mặt phẳng vuông góc với nhau
Trả lời bởi Mai Trung Hải Phong