Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.
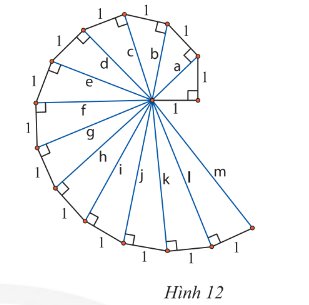
Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.

Chứng minh rằng tam giác \(ABC\) vuông trong các trường hợp sau:
a) \(AB = 8\)cm, \(AC = 15\)cm, \(BC = 17\)cm
b) \(AB = 29\)cm, \(AC = 21\)cm, \(BC = 20\)cm
c) \(AB = 12\)cm, \(AC = 37\), \(BC = 35\)cm
a) Ta có: \({8^2} + {15^2} = {17^2}\) suy ra \(A{B^2} + A{C^2} = B{C^2}\). Vậy tam giác \(ABC\) vuông tại \(A\)
b) Ta có: \({20^2} + {21^2} = {29^2}\) suy ra \(B{C^2} + A{C^2} = A{B^2}\). Vậy tam giác \(ABC\) vuông tại \(C\)
c) Ta có: \({12^2} + {35^2} = {37^2}\) suy ra \(A{B^2} + B{C^2} = A{C^2}\). Vậy tam giác \(ABC\) vuông tại \(B\)
Trả lời bởi Hà Quang MinhCho biết thang của một xe máy cứu hỏa có chiều dài \(13\)m, chân thang cách mặt đất \(3\)m và cách tường của toàn nhà \(5\)m. Tính chiều cao mà thang có thể vươn tới.
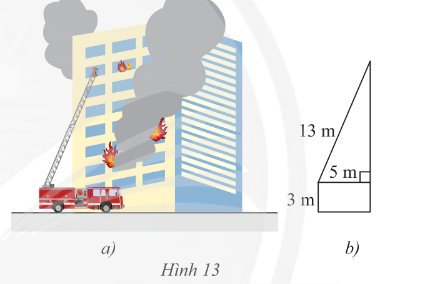
Gọi \(x\) là khoảng cách của xe đến đầu thang (m)
Áp dụng định lý Pythagore vào tam giác vuông trong hình ta có:
\({x^2} + {5^2} = {13^2}\)
\({x^2} = {13^2} - {5^2} = 144 = {12^2}\)
\(x = 12\) (m)
Chiều cao mà thang có thể vươn tới là:
\(12 + 3 = 15\) (m)
Trả lời bởi Hà Quang MinhMột con thuyền đang neo ở một điểm cách chân tháp hải đăng \(180\)m. Cho biết tháp hải đăng cao \(25\)m. Hãy tính khoảng cách từ thuyền đến đỉnh tháp hải đăng.

Gọi \(x\) là khoảng cách từ thuyền đến đỉnh tháp (m)
Áp dụng định lý Pythagore ta có:
\({x^2} = {180^2} + {25^2}\)
\({x^2} = 33025\)
\(x = \sqrt {33025} \approx 181,73\) (m)
Vậy khoảng cách từ thuyền đến đỉnh tháp hải đăng là: 181,73m
Trả lời bởi Hà Quang MinhCho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)
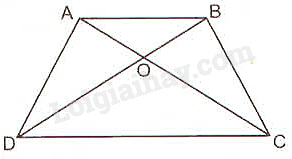
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
Trả lời bởi Hà Quang Minh

Trả lời bởi Mai Trung Hải Phong