Cho hình vuông ABCD có độ dài cạnh bằng 3cm. Tính độ dài của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \).
$3. Khái niệm vectơ
QL
Hướng dẫn giải
Thảo luận (1)
QL
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ overrightarrow a ,overrightarrow b ,overrightarrow c (Hình 47).a) Hãy chỉ ra các cặp vectơ cùng phương.b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.
Đọc tiếp
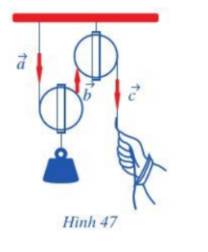
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)(Hình 47).
a) Hãy chỉ ra các cặp vectơ cùng phương.
b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.
Hướng dẫn giải
Thảo luận (1)

Gọi a, b, c là các đường thẳng lần lượt chứa các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \).
Khi đó: a, b, c lần lượt là giá của các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
a) Dễ thấy: a // b // c
\( \Rightarrow \) Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cùng phương với nhau.
Vậy các cặp vectơ cùng phương là: \(\overrightarrow a \) và \(\overrightarrow b \), \(\overrightarrow a \) và \(\overrightarrow c \), \(\overrightarrow b \) và \(\overrightarrow c \).
b) Quan sát ba vectơ, ta thấy: vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng xuống còn vectơ \(\overrightarrow b \) hướng lên trên.
Vậy vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng, vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, vectơ \(\overrightarrow b \) và \(\overrightarrow c \) ngược hướng.
Trả lời bởi Hà Quang Minh
Ta có: \(|\overrightarrow {AB} | = AB\) và \(|\overrightarrow {AC} |\; = AC.\)
Mà \(AB = 3,\;AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \)
\( \Rightarrow \;|\overrightarrow {AB} |\, = 3;\;\;|\overrightarrow {AC} |\, = 3\sqrt 2 \)
Trả lời bởi Hà Quang Minh