Mũi tên xuất phát từ A đến B trong Hình 34 mô tả chuyển động (có hướng) của một máy bay trên đường băng.
Đoạn thẳng AB có hướng được gọi là gì?

Mũi tên xuất phát từ A đến B trong Hình 34 mô tả chuyển động (có hướng) của một máy bay trên đường băng.
Đoạn thẳng AB có hướng được gọi là gì?

Trong công viên, để chỉ dẫn hướng đi và khoảng cách từ cổng đến khu vui chơi của trẻ em, người ta vẽ đoạn thẳng có mũi tên như Hình 35. Hình ảnh về mũi tên chỉ dẫn cho biết những thông tin gì?
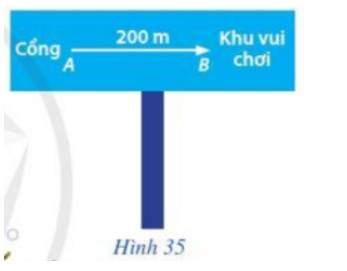
Hình ảnh về mũi tên chỉ dẫn cho biết:
+) Hướng đi từ Cổng đến Khu vui chơi: Đi sang phải
+) Khoảng cách từ Cổng đến Khu vui chơi: 200 m.
Trả lời bởi Hà Quang MinhCho tam giác ABC. Viết tất cả các vectơ mà điểm đầu và điểm cuối là A, B hoặc C.
Các vectơ đó là: \(\overrightarrow {AA} ,\;\overrightarrow {AB} ,\;\overrightarrow {AC} ,\;\overrightarrow {BA} ,\;\overrightarrow {BB} ,\;\overrightarrow {CC} ,\;\overrightarrow {CA} ,\;\overrightarrow {CB};\overrightarrow {BC} ,\;\overrightarrow {CC} .\)
Chú ý
+) vectơ \(\overrightarrow {AB} \ne \overrightarrow {BA} \)(khác nhau về hướng)
+) \(\overrightarrow {AA} \) cũng là một vectơ.
Trả lời bởi Hà Quang MinhQuan sát Hình 39 và cho biết vị trí tương đối giữa giá của vectơ \(\overrightarrow {CD} \) với giá của vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {PQ} \).
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Giá của vectơ \(\overrightarrow {PQ} \) là đường thẳng PQ.
Dễ thấy: AB // CD và CD trùng PQ.
Trả lời bởi Hà Quang MinhQuan sát hai biển báo ở Hình 40a, 40b, cho biết hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng hướng hay không.
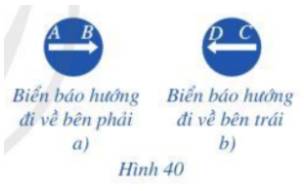
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: đường thẳng AB trùng với đường thẳng CD.
Do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng phương.
Lại có: vectơ \(\overrightarrow {AB} \) chỉ hướng đi về bên phải còn vectơ \(\overrightarrow {CD} \) chỉ hướng đi về bên trái.
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có ngược hướng.
Trả lời bởi Hà Quang MinhQuan sát hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ở hình 42.
a) Nhận xét về phương của hai vectơ đó.
b) Nhận xét về hướng của hai vectơ đó.
c) So sánh độ dài của hai vectơ đó.
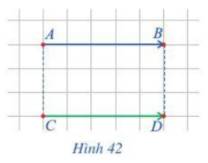
a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.
Trả lời bởi Hà Quang MinhCho tam giác ABC. Vẽ điểm D thỏa mãn \(\overrightarrow {AD} = \overrightarrow {BC} .\) Tứ giác ABCD là hình gì?
Ta có: \(\overrightarrow {AD} = \overrightarrow {BC} .\)
\( \Rightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
Do đó tứ giác ABCD có một cặp cạnh đối song và bằng nhau
Vậy tứ giác ABCD là hình bình hành.
Trả lời bởi Hà Quang MinhCho A, B, C là ba điểm thẳng hàng, B nằm giữa A và C. Viết các cặp vectơ cùng hướng, ngược hướng trong những vectơ sau: \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {CA} ,\overrightarrow {CB} .\)
Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
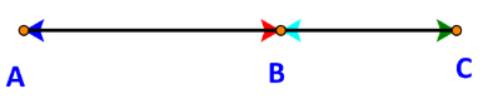
Dễ thấy:
Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)
Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).
Các cặp vectơ ngược hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);
Trả lời bởi Hà Quang MinhCho đoạn thẳng MN có trung điểm là I.
a) Viết các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I.
b) vectơ nào bằng \(\overrightarrow {MI} \)? Bằng \(\overrightarrow {NI} \)?
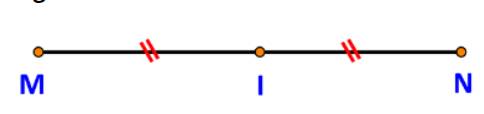
a) Các vectơ đó là: \(\overrightarrow {MI} ,\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {NI} ,\overrightarrow {MN} ,\overrightarrow {NM} \).
b) Dễ thấy:
+) vectơ \(\overrightarrow {IN} \)cùng hướng với vectơ \(\overrightarrow {MI} \). Hơn nữa: \(|\overrightarrow {IN} |\; = IN = MI = \;|\overrightarrow {MI} |\)
\( \Rightarrow \overrightarrow {IN} = \overrightarrow {MI} \)
+) vectơ \(\overrightarrow {IM} \)cùng hướng với vectơ \(\overrightarrow {NI} \). Hơn nữa: \(|\overrightarrow {IM} |\; = IM = NI = \;|\overrightarrow {NI} |\)
\( \Rightarrow \overrightarrow {IM} = \overrightarrow {NI} \)
Vậy \(\overrightarrow {IN} = \overrightarrow {MI} \) và \(\overrightarrow {IM} = \overrightarrow {NI} \).
Trả lời bởi Hà Quang MinhCho hình thang ABCD có hai đáy là AB và CD. Tìm vectơ:
a) Cùng hướng với \(\overrightarrow {AB} \)
b) Ngược hướng với \(\overrightarrow {AB} \)
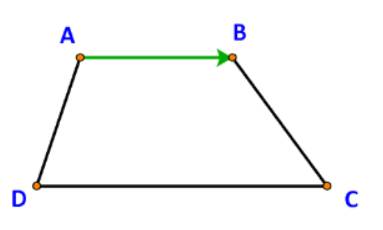
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB.
Các vectơ cùng phương với vectơ \(\overrightarrow {AB} \) là: \(\overrightarrow {CD} \) và \(\overrightarrow {DC} \)
a) vectơ \(\overrightarrow {DC} \) cùng hướng với vectơ \(\overrightarrow {AB} \).
b) vectơ \(\overrightarrow {CD} \) ngược hướng với vectơ \(\overrightarrow {AB} \).
Trả lời bởi Hà Quang Minh
Đoạn thẳng AB có hướng được gọi là vecto \(\overrightarrow {AB} \).
Trả lời bởi Hà Quang Minh