Cho hình bình hành ABCD có AB = a; BC = b; BD = m và AC = n.
Chứng minh rằng : \(m^2+n^2=2\left(a^2+b^2\right)\) ?
Cho hình bình hành ABCD có AB = a; BC = b; BD = m và AC = n.
Chứng minh rằng : \(m^2+n^2=2\left(a^2+b^2\right)\) ?
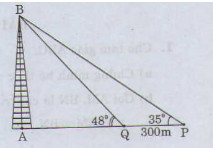
Hai chiếc tầu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đẳng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat{BPA}=35^0;\widehat{BQA}=48^0\). Tính chiều cao của tháp ?
Ta có: AQ = ABcot480
AP = ABcot350
QP = AB(cot350 - cot480)
=> AB = 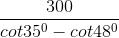 ≈
≈ 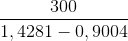
Tính được AB ≈ 568,50m
Trả lời bởi Anh TriêtTam giác ABC có \(\widehat{A}=120^0\). Tính cạnh BC cho biết cạnh AC =m và AB = n ?
Ta có: BC2 = AC2 + AB2 - 2AB.AC. cos1200
=> BC2 = m2 + n2 - 2m.n ()
=> BC2 = m2 + n2 + m.n
=> BC =
Trả lời bởi Anh Triêt
Cho tam giác ABC biết cạnh a = 137,5cm; \(\widehat{B}=83^0;\widehat{C}=57^0\). Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác ?
Ta có: = 1800 - (
+
) = 400
Áp dụng định lí sin :
=
=
, ta có:
b = ≈ 212,32cm
c = ≈ 179,40cm
Tam giác ABC có các cạnh a = 8cm, b = 10cm, c = 13 cm
a) Tam giác đó có góc tù không ?
b) Tính độ dài trung tuyến MA của tam giác ABC đó ?
a) Xét tổng a2 + b2 - c2 = 82 + 102 - 132 = -5 < 0
Vậy tam giác này có góc C tù
cos C = =
≈ -0, 3125 =>
= 91047’
b) Áp dụng công thức tính đường trung tuyến, ta tính được AM ≈ 10,89cm
Trả lời bởi Anh TriêtTính diện tích S của tam giác có số đo các cạnh lần lượt là 7,9 và 12 ?
Ta có 2p = 7 + 9 + 12 => p = 14
p - a = 14 - 7 = 7
p - b = 14 - 9 = 5
p - c = 12 - 12 = 2
Áp dụng công thức Hê ron:
S = =
= 14√5 (dvdt)
Cho tam giác ABC biết các cạnh \(a=52,1cm;b=85cm;c=54cm\). Tính các góc \(\widehat{A},\widehat{B},\widehat{C}\) ?
Từ định lí cosin a2 = b2 + c2 - 2bc. cosA
ta suy ra cos A = =
=> cosA ≈ 0,8089 => = 360
Tương tự, ta tính được ≈ 1060 28’ ;
≈ 370 32’.
Cho tam giác ABC vuông tại A, \(\widehat{B}=58^0\) và cạnh \(a=72cm\). Tính \(\widehat{C}\), cạnh b, cạnh c và đường cao \(h_a\) ?
= 320; b = a.cos320 => b ≈ 61,06cm; c = a.sin320 ≈ 38,15cm
ha = => ha ≈ 32,35cm
Cho tam giác ABC có \(\widehat{A}=120^0\), cạnh b = 8cm và cạnh c = 5cm. Tính cạnh a và các góc \(\widehat{B,}\widehat{C}\) của tam giác đó ?
a2 = 82 + 52 - 2.8.5 cos 1200 = 64 + 25 + 40 = 129
=> a = √129 ≈ 11, 36cm
Ta có thể tính góc B theo định lí cosin
cosB = =
≈ 0,7936 =>
= 37048’
Ta cũng có thể tính góc B theo định lí sin :
cosB = =
=> sinB ≈ 0,6085 =>
= 37048’
Tính C từ = 1800- (
+
) =>
≈ 22012’
Tính góc lớn nhất của tam giác ABC biết :
a) Các cạnh a = 3cm, b = 4cm và c = 6cm
b) Các cạnh a = 40cm, b = 13cm và c = 37cm
Ta biết trong tam giác thì đối diện với cạnh lớn nhất là góc lớn nhất, vậy trong câu a) góc lớn nhất là góc C còn trong câu b) góc lớn nhất là góc A
a) cos =
=
≈ -0,4583 =>
= 117016’
b)cos =
=
=>
= 93041’
Áp dụng định lí về đường trung tuyến:
OA2 = -
- 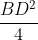 (1)
(1)
Thay OA =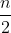 , AB = a, AD = BC = b và BD = m vào (1) ta có:
, AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)
Trả lời bởi Anh Triêt