Một tấm kẽm hình vuông ABCD có cạnh bằng 30cm. Người ta gập tấm kẽm theo 2 đường EF và GH cho đến khi AD và BC trùng nhau như hình vẽ dưới đây để được một lăng trụ khuyêt đáy.
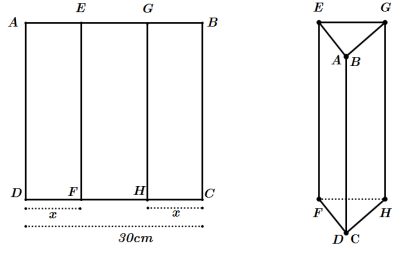
Giá trị của \(x\) để thể tích khối lăng trụ lớn nhất là
5 cm 9 cm 8 cm 10 cm Hướng dẫn giải:Hình lăng trụ được xét có chiều cao là AD = 30cm. Do đó thể tich lăng trụ sẽ lớn nhất khi và chỉ khi đáy AEG có diện tích lớn nhất. Áp dụng công thức Heron với \(p=30:2=15\), \(a=b=x;c=30-2x\) suy ra \(p-a=p-b=15-x\);\(p-c=15-\left(30-2x\right)=2x-15\) . Kí hiệu S là diện tích AEG thì
\(S^2=p\left(p-a\right)\left(p-b\right)\left(p-c\right)=15\left(15-x\right)^2\left(2x-15\right)\)
Tính giá trị biểu thức \(\left(15-x\right)^2\left(2x-15\right)\) tại \(x=5,8,9,10\) (bằng lệnh CALC) ta thấy khối lăng trụ có thể tích lớn nhất khi \(x=10\)
Cách khác: Xét hàm số \(f\left(x\right)=\left(15-x\right)^2\left(2x-15\right),x\in\left(\dfrac{15}{2};15\right)\)
\(f'\left(x\right)=2\left(x-15\right)\left(2x-15\right)+2\left(x-15\right)^2=\)\(2\left(x-15\right)\left(2x-15+x-15\right)=2\left(x-15\right)\left(3x-30\right)\)
Trong khoảng \(\left(\dfrac{15}{2};15\right)\), đạo hàm \(f'\left(x\right)\) chỉ triệt tiêu tại \(x=10\). Giá trị \(f\left(10\right)=125\)là GTLN của \(f\left(x\right)\)(tại hai đầu mút, giá trị hàm số bằng 0). Vì vậy \(S\) đạt giá trị lớn nhất khi và chỉ khi \(x=10\), khi đó thể tích khối lăng trụ cũng đạt lớn nhất.
.
