Cho hai hàm số \(f\left(x\right)=ax^3+bx^3+cx-\dfrac{1}{2}\) và \(g\left(x\right)=dx^2+ex+1\left(a,b,c,d,e\in\mathbb{R}\right).\) Biết rằng đồ thị của hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \(-3;-1;1\) như hình vẽ dưới đây
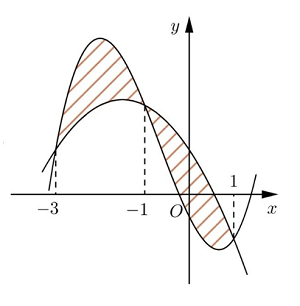
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
\(8\).\(4\).\(\dfrac{9}{2}\).\(5\).Hướng dẫn giải:Diện tích cần tính là \(S=\int^1_{-3}\left|f\left(x\right)-g\left(x\right)\right|\text{d}x.\) Từ giả thiết về các hệ số của \(f\left(x\right),g\left(x\right)\) suy ra \(f\left(x\right)-g\left(x\right)\) là một đa thức bậc ba có hệ số bậc ba là \(a,\)số hạng tự do là \(-\dfrac{3}{2}\) và phương trình bậc ba \(f\left(x\right)-g\left(x\right)=0\) có ba nghiệm phân biệt \(-3.-1,1\) nên \(f\left(x\right)-g\left(x\right)=a\left(x+3\right)\left(x^2-1\right)=ax^3+...+\dfrac{-3}{2}.\) Đồng nhất hệ số ta suy ra \(-3a=-\dfrac{3}{2}\Rightarrow a=\dfrac{1}{2}\), do đó
\(f\left(x\right)-g\left(x\right)=\dfrac{1}{2}\left(x+3\right)\left(x^2-1\right)\Rightarrow S=\dfrac{1}{2}\int^1_{-3}\left|\left(x+3\right)\left(x^2-1\right)\right|\text{d}x=4.\)
