Trong không gian Oxyz, sàn của một căn phòng có dạng hình tứ giác với bốn đỉnh O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), C(0; \(2\sqrt{2}\); 0). Bốn bức tường của căn phòng đều vuông góc với sàn.
a) Viết phương trình bốn mặt phẳng tương ứng chứa bốn bức tường đó.
b) Trong bốn mặt phẳng tương ứng chứa bốn bức tường đó, hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.

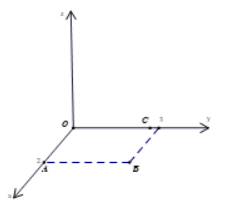
a) Bốn mặt phẳng tương ứng chứa bốn bức tường vuông góc với mặt sàn là: Mặt phẳng (Oyz), mặt phẳng (Oxz), mặt phẳng (P) chứa hai điểm A, B và vuông góc với mặt sàn, mặt phẳng (Q) chứa hai điểm B, C và vuông góc với mặt sàn.
Mặt phẳng (Oyz) có vectơ pháp tuyến \(\overrightarrow i \left( {1;0;0} \right)\) và đi qua điểm \(O\left( {0;0;0} \right)\) nên phương trình mặt phẳng (Oyz) là: \(x = 0\)
Mặt phẳng (Oxz) có vectơ pháp tuyến \(\overrightarrow j \left( {0;1;0} \right)\) và đi qua điểm \(O\left( {0;0;0} \right)\) nên phương trình mặt phẳng (Oxz) là: \(y = 0\)
Ta có: \(\overrightarrow {AB} \left( {0;3;0} \right),\overrightarrow {BC} \left( { - 2;2\sqrt 2 - 3;0} \right),\overrightarrow i \left( {1;0;0} \right),\overrightarrow j \left( {0;1;0} \right),\overrightarrow k \left( {0;0;1} \right)\)
Mặt phẳng (P) đi qua điểm A(2; 0; 0) và nhận \(\overrightarrow i = \left( {1;0;0} \right)\) làm vectơ pháp tuyến. Do đó, phương trình mặt phẳng (P) là: \(x - 2 = 0\)
\(\left[ {\overrightarrow {BC} ,\overrightarrow k } \right] = \left( {\left| {\begin{array}{*{20}{c}}{2\sqrt 2 - 3}&0\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 2}\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&{2\sqrt 2 - 3}\\0&0\end{array}} \right|} \right) = \left( {2\sqrt 2 - 3;2;0} \right)\)
Mặt phẳng (Q) đi qua điểm \(C\left( {0;2\sqrt 2 ;0} \right)\) và nhận \(\left[ {\overrightarrow {BC} ,\overrightarrow k } \right] = \left( {2\sqrt 2 - 3;2;0} \right)\) làm vectơ pháp tuyến. Do đó, phương trình mặt phẳng (Q) là:
\(\left( {2\sqrt 2 - 3} \right)x + 2\left( {y - 2\sqrt 2 } \right) = 0 \Leftrightarrow \left( {2\sqrt 2 - 3} \right)x + 2y - 4\sqrt 2 = 0\)
b) Các cặp mặt phẳng vuông góc với nhau là: (Oxz) và (Oyz); (Oxz) và (P).

