\(\begin{array}{l}a)\frac{{{3^{12}} + {3^{15}}}}{{1 + {3^3}}}\\ = \frac{{{3^{12}} + {3^{12}}{{.3}^3}}}{{1 + {3^3}}}\\ = \frac{{{3^{12}}.(1 + {3^3})}}{{1 + {3^3}}}\\ = {3^{12}}\\b)2:{\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 0,{125^3}{.8^3} - {( - 12)^4}:{6^4}\\ = 2:{\left( {\frac{3}{6} - \frac{4}{6}} \right)^2} + {(0,125.8)^3} - {12^4}:{6^4}\\ = 2:{\left( {\frac{{ - 1}}{6}} \right)^2} + {1^3} - {(\frac{{12}}{6})^4}\\ = 2:\frac{1}{{36}} + 1 - {2^4}\\ = 2.36 + 1 - 16\\ = 72 + 1 - 16=57\end{array}\)
Bài tập cuối chương I
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
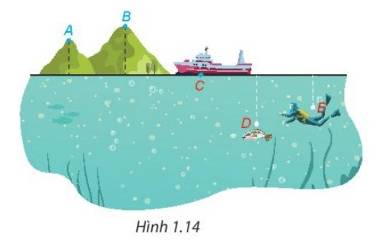
Hình 1.14 mô phỏng vị trí của năm điểm A,B,C,D,E so với mực nước biển. Biết rằng độ cao (tính theo đơn vị kilomet) so với mực nước biển của mỗi điểm là một trong các số sau:
\(\frac{{33}}{{12}};\frac{{79}}{{30}}; - \frac{{25}}{{12}}; - \frac{5}{6};0.\)
Chị Trang đang có ba tháng thực tập tại Mĩ. Gần hết thời gian thực tập, chị Trang và bạn có kế hoạch tổ chức một bữa tiệc chia tay trước khi về nước. Chị ấy dự định mua 4 cái bánh pizza, mỗi cái giá 10,25 USD. Chị Trang có phiếu giảm giá 1,5 USD cho mỗi cái bánh pizza, hãy tính tổng số tiền chị ấy dùng để mua bánh.
Bố của Hà chuẩn bị đi công tác bằng máy bay. Theo kế hoạch, máy bay sẽ cất cánh lúc 14 giờ 40 phút chiều. Bố của Hà cần phải có mặt ở sân bay trước ít nhất 2 giờ để làm thủ tục, biết rằng đi từ nhà Hà đến sân bay mất khoảng 45 phút. Hỏi bố của Hà phải đi từ nhà muộn nhất là lúc mấy giờ để đến sân bay cho kịp giờ bay?
