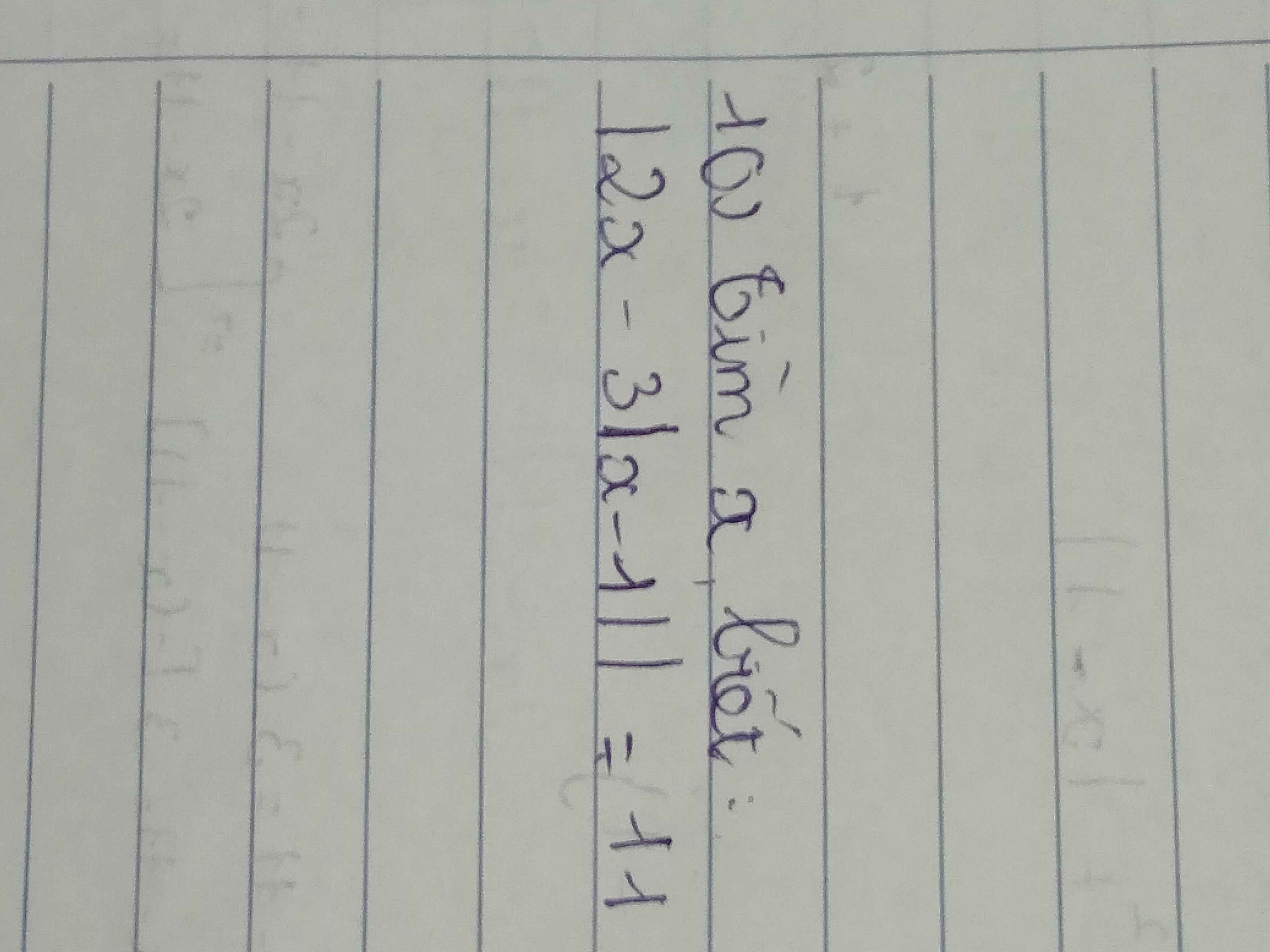\(\left(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{8.9.10}\right)x=\frac{22}{45}\)
\(\Rightarrow\frac{1}{2}\left(\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{8.9.10}\right)x=\frac{22}{45}\)
\(\Rightarrow\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{8.9}-\frac{1}{9.10}\right)x=\frac{44}{45}\)
\(\Rightarrow\left(\frac{1}{1.2}-\frac{1}{9.10}\right)x=\frac{44}{45}\)
\(\Rightarrow\left(\frac{1}{2}-\frac{1}{90}\right)x=\frac{44}{45}\)
\(\Rightarrow\frac{22}{45}.x=\frac{44}{45}\)
\(\Rightarrow x=2\)
Vậy \(x=2\)