Xét \(\Delta\)EBC và \(\Delta\) DBC có :
BC chung
góc BEC = góc CDB (= 90 độ)
góc EBC = góc DCB ( \(\Delta\)ABC cân tại A )
Do đó , \(\Delta\)EBC = \(\Delta\)DCB ( cạnh huyền - góc nhọn )
=> EB = DC ( 2 cạnh tương ứng )
Ta có : AE + EB = AB
AD + DC = AC
mà EB = DC ( cmt )
AB = AC ( tam giác ABC cân tại A )
=> AE = AD ( đpcm )
Cậu vẽ hình đi mình sẽ nghĩ cách giải giúp bạn! :)
Kẻ AH \(\perp\)BC (1)
Gọi Giao điểm của AH và ED là T
Cách làm của mình , bạn tham khảo nhé :
Chứng minh tam giác AIE = tam giác AID ( cạnh huyền - cạnh góc vuông )
=> góc EAI = góc IAD ( 2 góc tương ứng )
Xét tam giác ATE và tam giác ATD có : AE = AD ; hai góc A bằng nhau ; AT chung => tam giác ATE = tam giác ATD ( c-g-c)
=> góc ATE = góc ATD ( 2 góc tương ứng )
mà góc ATE + góc ATD = 180 độ
=> góc ATE = góc ATD = 180 độ / 2 = 90 độ
=> AT \(\perp\)ED
=> AH \(\perp\)ED (2)( A , H , T thẳng hàng - nếu cần thì chứng minh)
Từ (1) và (2) => ED // BC ( từ vuông góc đến song song )![]()
câu d) bạn so sánh AI với IB theo định lý pitago ...
So sánh BE với AD ( AI = BI cmt ; EI = ID ( chứng minh tam giác )
Hiểu chưa ạ ?![]()




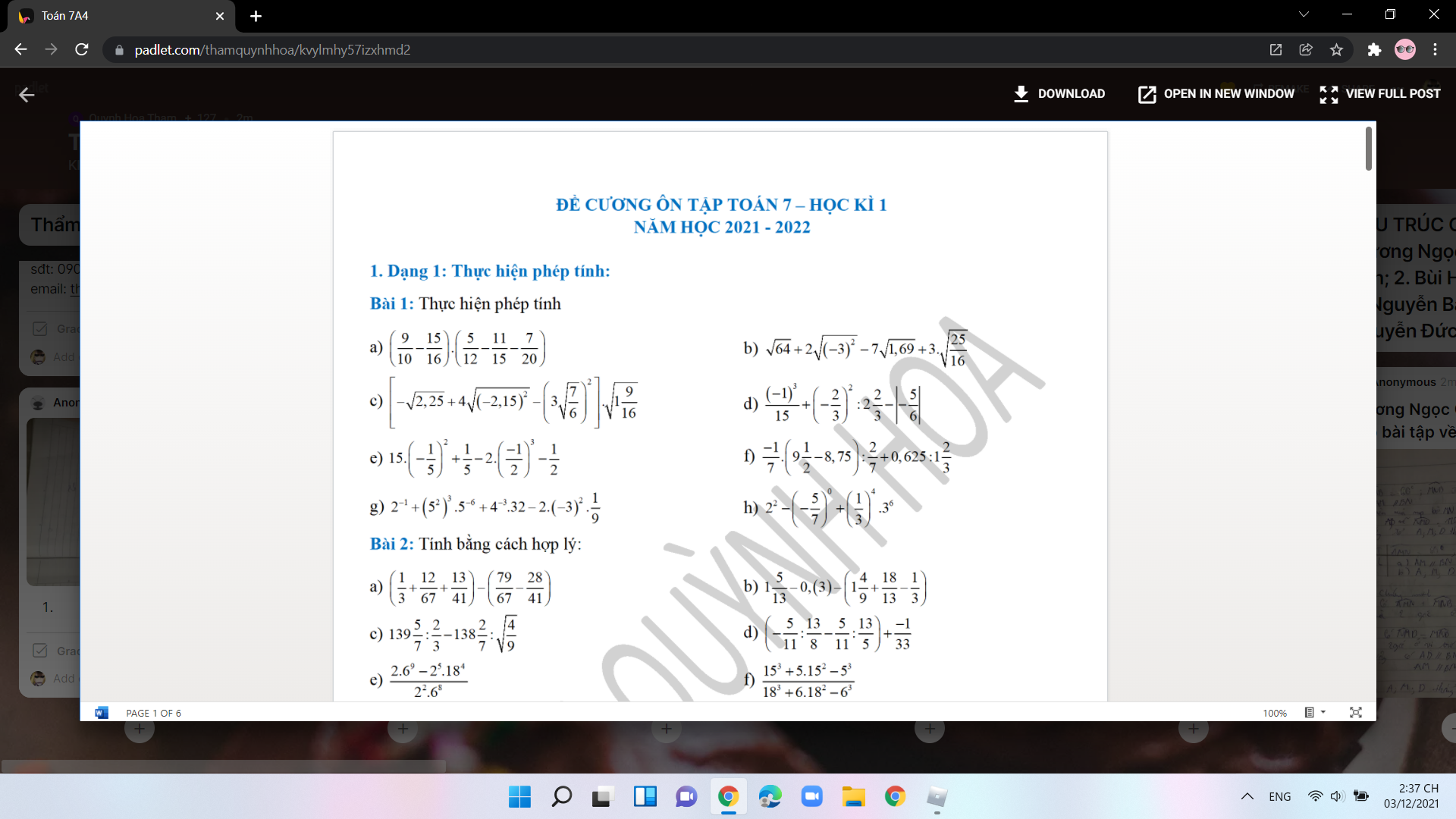 làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc )
làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc )


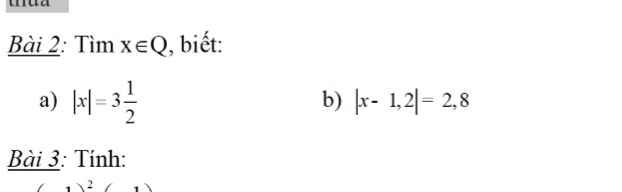
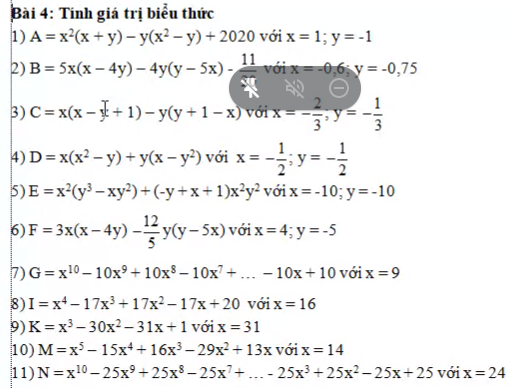



 mình bài 9,10,11 nhé các bạn thân yêu
mình bài 9,10,11 nhé các bạn thân yêu