Bài 73:
Do đây là hình hộp đứng nên:
\(V_{ABCD.A'B'C'D'}=AA'.S_{A'B'C'D'}=AA'.S_1\) \((1)\)
Lại có: do hình hộp dạng đứng nên \(A'C', CC'\perp \) đáy, kéo theo \(A'C';CC'\perp AC,A'C'\Rightarrow ACC'A'\) là hình chữ nhật
Tương tự, \(BDD'B'\) là hình chữ nhật
\(\Rightarrow \left\{\begin{matrix} S_2=S_{ACC'A'}=A'C'.AA'\\ S_3=S_{BDD'B'}=BB'.B'D'=AA'.B'D'\end{matrix}\right.\)
\(\Rightarrow S_2S_3=AA'^2.A'C'.B'D'=AA'.2S_1\Leftrightarrow AA'=\sqrt{\frac{S_2S_3}{2S_1}}(2)\)
\((1),(2)\Rightarrow V_{ABCD.A'B'C'D'}=\sqrt{\frac{S_2S_3}{2S_1}}.S_1=\sqrt{\frac{S_1S_2S_3}{2}}\)
Đáp án A
Bài 74: Vì là hình lập phương nên tất cả các mặt của nó đều là hình vuông cạnh a.
Vì $O$ là tâm hình lập phương nên \(d(O,(AA'B'))=\frac{1}{2}AD=\frac{1}{2}a\)
\(\Rightarrow V_{AA'B'O}=\frac{1}{3}d(O,(AA'B')).S_{AA'B'}=\frac{1}{3}.\frac{a}{2}.\frac{a.a}{2}=\frac{a^3}{12}\)




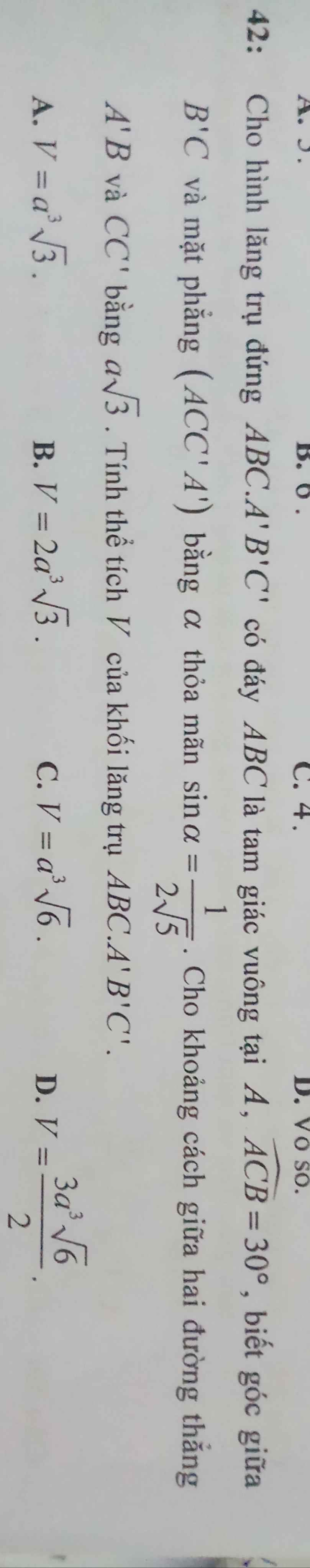
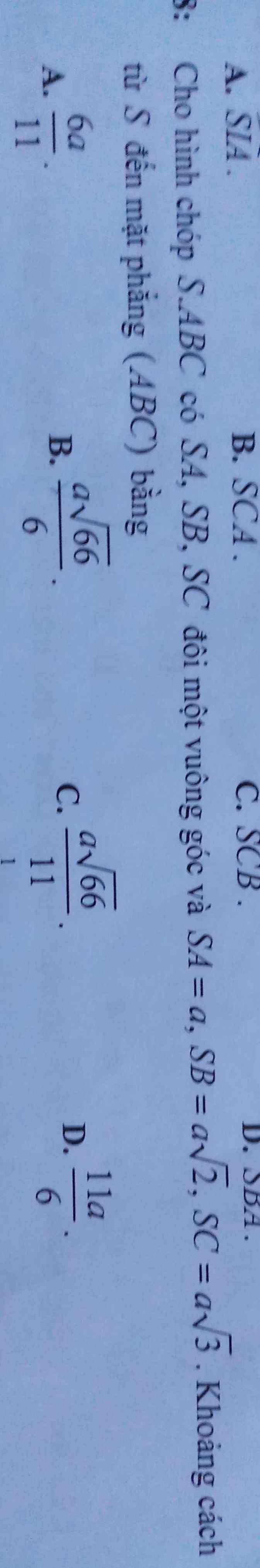


 Giải giúp em câu hai với câu 3 nha
Giải giúp em câu hai với câu 3 nha
