\(\left|x+2\right|=x\Rightarrow\left\{{}\begin{matrix}x+2=-x\forall x\ge0\\x+2=x\forall x\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+x=-2\\x-x=-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=-2\forall x\ge0\\0x=-2\forall x\ge0\end{matrix}\right.\)
\(\Rightarrow x\in\varnothing\)
Cách khác:
Với mọi giá trị của x ta có:
\(\left|x+2\right|\ge0\Rightarrow x\ge0\)
\(\Rightarrow x+2>0\Rightarrow\left|x+2\right|=x+2\)
Ta có:
\(x+2=x\Rightarrow x-x=-2\Rightarrow0x=-2\Rightarrow x\in\varnothing\)
Vậy............
Chúc bạn học tốt!!!
Ta có: \(\left|x+2\right|=x\)
\(\Rightarrow\left[{}\begin{matrix}x+2=x\\x+2=-x\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x-x=-2\\x+x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}0=-2\\2x=-2\end{matrix}\right.\)vô lý vì \(0\ne-2\)
Vậy \(\Rightarrow x=-1\)
Vậy \(x=-1\)
\(\left|x+2\right|=x\)
\(\left[{}\begin{matrix}x+2=x\left(với\:x\ge-2\right)\\x+2=-x\left(với\:x< -2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}0x=-2\left(vô\:nghiệm\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
vậy phương trình vô nghiệm
\(\left|x+2\right|=x\)
\(\Rightarrow\left\{{}\begin{matrix}x+2=-x\\x+2=x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-2x=2\Rightarrow x=-1\\x=2\end{matrix}\right.\)
Nhưng với x=2 ko TM
\(\Rightarrow x=-1\)


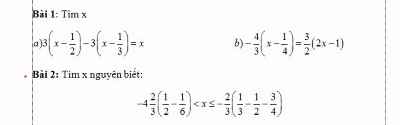 giúp mik giải 2 bài này vs ạ
giúp mik giải 2 bài này vs ạ