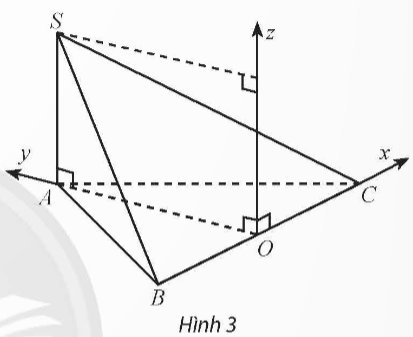
a) \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\overrightarrow {OA} = \frac{{a\sqrt 3 }}{2}\overrightarrow j = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)
\(\overrightarrow {OB} = - \frac{a}{2}\overrightarrow i = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)
\(\overrightarrow {OC} = \frac{a}{2}\overrightarrow i = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)
\(\overrightarrow {OS} = \frac{{a\sqrt 3 }}{2}\overrightarrow j + a\overrightarrow k = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)
b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)