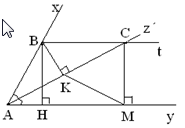
+ Vì \(Az\) là tia phân giác của \(\widehat{BAM}\left(gt\right)\)
Mà \(C\in Az.\)
=> \(AC\) là tia phân giác của \(\widehat{BAM}.\)
=> \(\widehat{BAC}=\widehat{MAC}=\frac{\widehat{BAM}}{2}\)
=> \(\widehat{BAC}=\widehat{MAC}=\frac{60^0}{2}=30^0.\)
Vì \(Bt\) // \(Ay\left(gt\right)\)
=> \(BC\) // \(AM.\)
=> \(\widehat{BCA}=\widehat{MAC}\) (vì 2 góc so le trong).
Mà \(\widehat{BAC}=\widehat{MAC}\left(cmt\right)\)
=> \(\widehat{BCA}=\widehat{BAC}.\)
Hay \(\widehat{BCK}=\widehat{BAK}.\)
+ Vì \(\Delta AKB\) vuông tại \(K\left(gt\right)\)
=> \(\widehat{ABK}+\widehat{BAK}=90^0\) (tính chất tam giác vuông).
+ Vì \(\Delta CKB\) vuông tại \(K\left(gt\right)\)
=> \(\widehat{CBK}+\widehat{BCK}=90^0\) (tính chất tam giác vuông).
=> \(\widehat{ABK}+\widehat{BAK}=\widehat{CBK}+\widehat{BCK}\left(=90^0\right).\)
Mà \(\widehat{BAK}=\widehat{BCK}\left(cmt\right).\)
=> \(\widehat{ABK}=\widehat{CBK}.\)
Xét 2 \(\Delta\) vuông \(AKB\) và \(CKB\) có:
\(\widehat{AKB}=\widehat{CKB}=90^0\left(gt\right)\)
Cạnh KB chung
\(\widehat{BAK}=\widehat{BCK}\left(cmt\right)\)
=> \(\Delta AKB=\Delta CKB\) (cạnh góc vuông - góc nhọn kề).
=> \(AK=CK\) (2 cạnh tương ứng).
+ Vì \(Az\) là tia phân giác của \(\widehat{BAH}\left(gt\right)\)
Mà \(K\in Az\)
=> \(AK\) là tia phân giác của \(\widehat{BAH}.\)
=> \(\widehat{BAK}=\widehat{HAK}=\frac{\widehat{BAH}}{2}.\)
=> \(\widehat{BAK}=\widehat{HAK}=\frac{60^0}{2}=30^0.\)
+ Vì \(\Delta AHB\) vuông tại \(H\left(gt\right)\)
=> \(\widehat{ABH}+\widehat{BAH}=90^0\) (tính chất tam giác vuông).
=> \(\widehat{ABH}+60^0=90^0\)
=> \(\widehat{ABH}=90^0-60^0\)
=> \(\widehat{ABH}=30^0.\)
Mà \(\widehat{BAK}=30^0\left(cmt\right)\)
=> \(\widehat{ABH}=\widehat{BAK}=30^0.\)
Xét 2 \(\Delta\) vuông \(BAH\) và \(ABK\) có:
\(\widehat{AHB}=\widehat{BKA}=90^0\left(gt\right)\)
Cạnh AB chung
\(\widehat{ABH}=\widehat{BAK}\left(cmt\right)\)
=> \(\Delta BAH=\Delta ABK\) (cạnh huyền - góc nhọn).
=> \(BH=AK\) (2 cạnh tương ứng).
Ta có:
\(\left\{{}\begin{matrix}BH\perp Ay\left(gt\right)\\CM\perp Ay\left(gt\right)\end{matrix}\right.\)
=> \(BH\) // \(CM\) (từ vuông góc đến song song).
Vì \(Bt\) // \(Ay\left(gt\right)\)
=> \(BC\) // \(HM.\)
Mà \(BH\) // \(CM\left(cmt\right)\)
=> \(BH=CM\) (tính chất đoạn chắn).
Mà \(\left\{{}\begin{matrix}BH=AK\left(cmt\right)\\AK=CK\left(cmt\right)\end{matrix}\right.\)
=> \(CK=CM.\)
=> \(\Delta KMC\) cân tại \(C\) (1).
+ Vì \(\Delta ACM\) vuông tại \(M\left(gt\right)\)
=> \(\widehat{MAC}+\widehat{ACM}=90^0\) (tính chất tam giác vuông).
=> \(30^0+\widehat{ACM}=90^0\)
=> \(\widehat{ACM}=60^0.\)
Hay \(\widehat{KCM}=60^0\) (2).
Từ (1) và (2) => \(\Delta KMC\) là tam giác đều (đpcm).
Chúc bạn học tốt!
t/g AHB vuông tại H có: ABH + BAH = 90o
=> ABH + 60o = 90o
=> ABH = 30o
= BAK
Dễ dàng c/m t/g BAH = t/g ABK ( cạnh huyền - góc nhọn)
=> BH = AK (2 cạnh tương ứng)
Có: BH _|_ Ay (gt)
CM _|_ Ay (gt)
=> BH // CM
Lại có: BC // HM (gt)
=>BH = CM ( tính chất đoạn chắn)
= AK = KC
=> t/g KMC cân tại C (1)
T/g ACM vuông tại M có: CAM + ACM = 90o
=> 30o + ACM = 90o
=> ACM = 60o (2)
Từ (1) và (2) => t/g KMC đều (đpcm)


