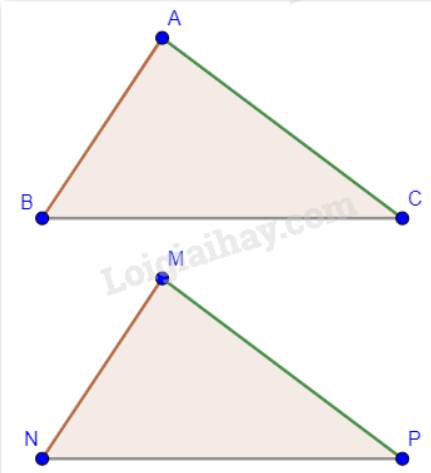
Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \)hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)
Vậy số đo góc P là 55°.