Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
Luyện tập chung trang 90
H24
Hướng dẫn giải
Thảo luận (1)
H24
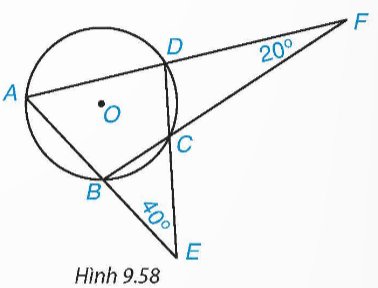
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết \(\widehat{BEC}\) = 40° và \(\widehat{DFC}\) = 20°, tính số đo các góc của tứ giác ABCD.
Hướng dẫn giải
Thảo luận (1)
Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat A + \widehat {BCD} = {180^o} \Rightarrow \widehat {BCD} = {180^o} - \widehat A\)
Tam giác ADE có:
\(\widehat {ADC} = {180^o} - \widehat E - \widehat A = {140^o} - \widehat A\)
Tam giác ABF có:
\(\widehat {ABC} = {180^o} - \widehat F - \widehat A = {160^o} - \widehat A\)
Tứ giác ABCD có:
\(\widehat A + \widehat {BCD} + \widehat {ABC} + \widehat {ADC} = {360^o}\)
\( \Rightarrow \widehat A + {180^o} - \widehat A + {140^o} - \widehat A + {160^o} - \widehat A = {360^o}\)
\( \Rightarrow {480^o} - 2\widehat A = {360^o} \Rightarrow \widehat A = {60^o}\)
Do đó, \(\widehat {BCD} = {120^o},\widehat {ADC} = {80^o},\widehat {ABC} = {100^o}\)
Trả lời bởi datcoder
H24
Cho hình vuông ABCD có cạnh bằng 4 cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.
Hướng dẫn giải
Thảo luận (1)

Gọi O là tâm của hình vuông ABCD. Do đó, đường tròn ngoại tiếp hình vuông ABCD là đường tròn tâm O, bán kính OD.
Áp dụng định lí Pythagore vào tam giác ADB vuông tại A có:
\(A{B^2} + A{D^2} = D{B^2} \Rightarrow DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \left( {cm} \right) \Rightarrow OD = 2\sqrt 2 \left( {cm} \right)\)
Chu vi đường tròn ngoại tiếp hình vuông ABCD là:
\({C_1} = \pi .DB = 4\sqrt 2 \pi \left( {cm} \right)\)
Diện tích hình tròn ngoại tiếp hình vuông ABCD là:
\({S_1} = \pi .O{D^2} = \pi .{\left( {2\sqrt 2 } \right)^2} = 8\pi \left( {c{m^2}} \right)\)
Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.
Tam giác AOB có: \(OA = OB\) (bán kính đường tròn (O)) nên tam giác OAB cân tại O. Do đó, OE là đường trung tuyến đồng thời là đường cao.
Do đó, \(OE \bot AB \Rightarrow \widehat {OEA} = \widehat {OEB} = {90^o}\)
Chứng minh tương tự ta có:
\(\widehat {OFB} = \widehat {OFC} = \widehat {OGC} = \widehat {OGD} = \widehat {OHD} = \widehat {OHA} = {90^o}\)
Tứ giác AEOH có: \(\widehat {HAE} = \widehat {OEA} = \widehat {OHA} = {90^o}\) nên tứ giác AEOH là hình chữ nhật.
Mà AO là tia phân giác của góc HAE (do ABCD là hình vuông) nên AEOH là hình vuông.
Do đó, \(OE = OH\).
Chứng minh tương tự ta có:
\(OE = OF,OF = OG,OG = OH\)
Do đó: \(OE = OH = OF = OG\). Suy ra, đường tròn (O; OE) nội tiếp hình vuông ABCD.
Ta có: \(OE = AE = \frac{{AB}}{2} = 2cm\)
Chu vi đường tròn nội tiếp hình vuông ABCD là:
\({C_2} = 2\pi .OE = 2\pi .2 = 4\pi \left( {cm} \right)\)
Diện tích hình tròn nội tiếp hình vuông ABCD là:
\({S_2} = \pi .O{E^2} = \pi {.2^2} = 4\pi \left( {c{m^2}} \right)\)
Trả lời bởi datcoder
H24
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
a) Vẽ đa giác EAFBGCHD.
b) Đa giác EAFBGCHD có phải là một bát giác đều hay không? Vì sao?
Hướng dẫn giải
Thảo luận (1)

a) + Vẽ đường tròn (O). Trên đường tròn vẽ hình vuông ABCD sao cho các đỉnh A, B, C, D theo thứ tự ngược chiều kim đồng hồ.
+ Vẽ điểm E thuộc đường tròn (O) sao cho \(\widehat {AOE} = {45^o}\) và tia OA quay thuận theo chiều kim đồng hồ đến tia OE.
+ Xác định các điểm F, G, H tương tự như xác định điểm E. Nối A với E, E với D, D với H, H với C, C với G, G với B, B với F, F với A ta được đa giác EAFBGCHD.
b) Vì A, E, D, H, C, G, B, F cùng thuộc (O) nên
\(OA = OE = OD = OH = OC = OG = OB = OF\)
Vì ABCD là hình vuông nên
\(\widehat {AOD} = \widehat {DOC} = \widehat {BOC} = \widehat {BOA} = {90^o}\)
Lại có: \(\widehat {AOE} = \widehat {BOF} = \widehat {COG} = \widehat {DOH} = {45^o}\) nên \(\widehat {DOE} = \widehat {AOF} = \widehat {BOG} = \widehat {COH} = {45^o}\)
Ta có:
\(\Delta AOE = \Delta DOE = \Delta DOH = \Delta COH = \Delta COG = \Delta BOG = \Delta BOF = \Delta AOF\left( {c.g.c} \right)\)
Suy ra:
+) \(AE = ED = DH = HC = CG = BG = BF = FA\)
+) \(\widehat {OAE} = \widehat {OEA} = \widehat {OED} = \widehat {ODE} = \widehat {ODH} = \widehat {OHD} = \widehat {OHC} = \widehat {OCH} = \widehat {OCG} = \widehat {OGC} = \widehat {OGB} = \widehat {OBG}\)\( = \widehat {OBF} = \widehat {OFB} = \widehat {OFA} = \widehat {FAO}\)
Do đó, \(\widehat {FAE} = \widehat {AED} = \widehat {EDH} = \widehat {DHC} = \widehat {HCG} = \widehat {CGB} = \widehat {GBF} = \widehat {BFA}\)
Đa giác EAFBGCHD có
\(\widehat {FAE} = \widehat {AED} = \widehat {EDH} = \widehat {DHC} = \widehat {HCG} = \widehat {CGB} = \widehat {GBF} = \widehat {BFA}\) và \(AE = ED = DH = HC = CG = BG = BF = FA\) nên đa giác EAFBGCHD là hình bát giác đều.
Trả lời bởi datcoder
H24
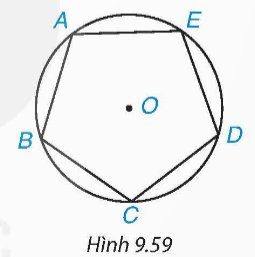
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như Hình 9.59.
a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C.
b) Phép quay trên sẽ biến các điểm B, C, D, E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?
Hướng dẫn giải
Thảo luận (1)
a) Phép quay chiều thuận \({216^o}\) tâm O biến điểm A thành điểm C.
b) Phép quay chiều thuận \({216^o}\) tâm O biến điểm E thành điểm B, điểm D thành điểm A, điểm C thành điểm E, điểm B thành điểm D. Do đó, phép quay này giữ nguyên ngũ giác đều ABCDE.
Trả lời bởi datcoder
H24
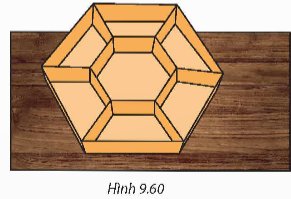
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10 cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
Hướng dẫn giải
Thảo luận (1)
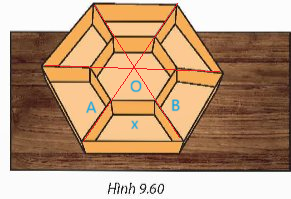
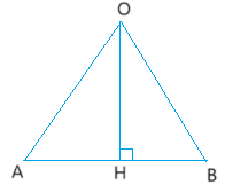
Nối các cặp đỉnh đối diện của lục giác với nhau, ta được điểm O là tâm của hình lục giác lớn và lục giác nhỏ.
Ta chia hình lục giác thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm) \(\left( {0 < x < 10} \right)\).
Khi đó \(\Delta AOB\) đều có \(OA = OB = AB = x\) và \(\widehat B = 60^\circ \).
Kẻ \(OH \bot AB\). Dựa vào hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
\(OH = OB.\sin \widehat {OBA} = x.\sin 60^\circ = \frac{{\sqrt 3 }}{2}x\left( {cm} \right)\)
Suy ra \({S_{\Delta AOB}} = \frac{{OH.AB}}{2} = \frac{{\frac{{\sqrt 3 }}{2}x.x}}{2} = \frac{{{x^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Ta có diện tích hình lục giác đều nhỏ là:
Slục giác đều nhỏ \( = 6.{S_{\Delta AOB}} = 6.\frac{{{x^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\).
Theo đề bài, diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
Shình thang = Slục giác đều nhỏ : 2 = \(\frac{{3\sqrt 3 {x^2}}}{2}:2 = \frac{{3\sqrt 3 {x^2}}}{4}\left( {c{m^2}} \right)\),
suy ra tổng diện tích 6 hình thang là: \(6.\frac{{3\sqrt 3 {x^2}}}{4} = \frac{{9\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\)
Do đó, diện tích lục giác đều lớn là:
Slục giác đều lớn = Slục giác đều nhỏ + S6 hình thang \( = \frac{{3\sqrt 3 {x^2}}}{2} + \frac{{9\sqrt 3 {x^2}}}{2} = \frac{{12\sqrt 3 {x^2}}}{2} = 6\sqrt 3 {x^2}\left( {c{m^2}} \right)\) (1)
Mà tương tự như Slục giác đều nhỏ, ta cũng có thể tính được diện tích lục giác đều theo độ dài cạnh của nó theo công thức \(S = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\) với x là độ dài cạnh.
Suy ra Slục giác đều lớn \( = \frac{{3\sqrt 3 {{.10}^2}}}{2} = 150\sqrt 3 \left( {c{m^2}} \right)\) (2)
Từ (1) và (2), ta có phương trình: \(6\sqrt 3 {x^2} = 150\sqrt 3 \)
suy ra \({x^2} = 25\), do đó \(x = 5\)(thỏa mãn vi \(0 < x < 10\)).
Vậy cạnh của lục giác đều nhỏ là 5cm.
Trả lời bởi datcoder
⦁ Vì ∆BEC vuông tại E (do BE ⊥ AC) nên tam giác có đường tròn ngoại tiếp đường tròn đường kính BC. Do đó ba điểm B, E, C cùng nằm trên đường tròn đường kính BC.
Vì ∆BFC vuông tại F (do CF ⊥ AB) nên tam giác có đường tròn ngoại tiếp là đường tròn đường kính BC. Do đó ba điểm B, F, C cùng nằm trên đường tròn đường kính BC.
Suy ra bốn điểm B, C, E, F cùng nằm trên một đường tròn hay tứ giác BCEF là tứ giác nội tiếp.
⦁ Chứng minh tương tự, ta cũng có tứ giác CAFD nội tiếp đường tròn đường kính AC và tứ giác ABDE nội tiếp đường tròn đường kính AB.
Trả lời bởi datcoder