Cho tam giác ABC vuông tại A có AC = 10 cm, \(\widehat C = {60^o}\). Độ dài hai cạnh còn lại là:
A. \(AB = \frac{{5\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)
B. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{14\sqrt 3 }}{3}cm\)
C. \(AB = 10\sqrt 3 cm;BC = 20cm\)
D. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)

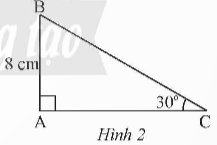




Xét tam giác ABC vuông tại A, \(\widehat C = {60^o}\), ta có:
\(AB = tan\widehat C. AC = tan{60^o}. 10 = 10\sqrt 3 \) cm
\(BC = \frac{{AB}}{{\sin \widehat C}} = \frac{{10\sqrt 3}}{{\sin {{60}^o}}} = 20\)cm.
Chọn đáp án C.
Trả lời bởi datcoder