Giải các phương trình sau:
\(\begin{array}{*{20}{l}}{a){\rm{ }}tanx = 0;}\\{b){\rm{ }}tan\left( {30^\circ --3x} \right) = tan75^\circ .}\end{array}\)
Giải các phương trình sau:
\(\begin{array}{*{20}{l}}{a){\rm{ }}tanx = 0;}\\{b){\rm{ }}tan\left( {30^\circ --3x} \right) = tan75^\circ .}\end{array}\)
Trong mặt phẳng toạ độ Oxy, cho C là điểm trên trục côtang có toạ độ là (-1; 1) (Hình 7). Những điểm nào biểu diễn góc lượng giác x có \(cotx = - 1\)? Xác định số đo của các góc lượng giác đó.
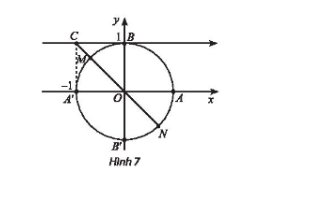
Trên đường tròn lượng giác hai điểm M và N biểu diễn các góc lượng giác có số đo góc x thỏa mãn \(cotx = - 1\).
Điểm M biểu diễn các góc lượng giác có số đo góc \(\frac{{3\pi }}{4} + k2\pi ,k \in \mathbb{Z}\).
Điểm N biểu diễn các góc lượng giác có số đo góc \( - \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}\).
Trả lời bởi Quoc Tran Anh LeGiải các phương trình sau:
\(\begin{array}{l}a)\;sinx = \frac{{\sqrt 3 }}{2}\\b)\;sin(x + {30^o}) = sin(x + {60^o})\end{array}\)
\(a)\;sinx = \frac{{\sqrt 3 }}{2}\)
Vì \(sin\frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\) nên \(sinx = \frac{{\sqrt 3 }}{2} \Leftrightarrow sin\frac{\pi }{3} = sin\frac{\pi }{3}\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \pi - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)
Vậy phương trình có nghiệm là \(x = \frac{\pi }{3} + k2\pi \) hoặc \(x = \frac{{2\pi }}{3} + k2\pi \)\(,k \in \mathbb{Z}\).
\(\begin{array}{l}b)\;sin(x + {30^o}) = sin(x + {60^o})\\ \Leftrightarrow \left[ \begin{array}{l}x + {30^o} = x + {60^o} + k{360^o},k \in \mathbb{Z}\\x + {30^o} = {180^o} - x - {60^o} + k{360^o},k \in \mathbb{Z}\end{array} \right.\\ \Leftrightarrow x = {45^o} + k{180^o},k \in \mathbb{Z}.\end{array}\)
Vậy phương trình có nghiệm là \(x = {45^o} + k{180^o},k \in \mathbb{Z}\).
Trả lời bởi Quoc Tran Anh LeTrong mặt phẳng toạ độ Oxy, cho T là điểm trên trục tang có toạ độ là \(\left( {1;\sqrt 3 } \right)\) (Hình 5). Những điểm nào trên đường tròn lượng giác x có \(tanx = \sqrt 3 \)?Xác định số đo của các góc lượng giác đó.
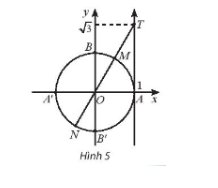
Những điểm biểu diễn góc x trên đường tròn lượng giác có \(tanx = \sqrt 3 \) là M và N.
Điểm M là điểm biểu diễn các góc lượng giác có số đo \(\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
Điểm N là điểm biểu diễn các góc lượng giác có số đo \( - \frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}\).
Trả lời bởi Quoc Tran Anh LeTrong Hình 3, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\)? Xác định số đo của các góc lượng giác đó.
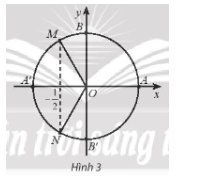
Điểm biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\) là M và N.
Số đo góc lượng giác có điểm biểu diễn M là: \(\frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Số đo góc lượng giác có điểm biểu diễn N là: \(\frac{{4\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Trả lời bởi Quoc Tran Anh Lea) Có giá trị nào của x để \(sinx = 1,5\)không?
b) Trong Hình 1, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có \(sinx = 0,5\)? Xác định số đo của các góc lượng giác đó.
a, Với mọi \(x\in R\), ta có: \(-1\le sin\left(x\right)\le1\)
Do đó, không có giá trị nào của x để \(sin\left(x\right)=1,5\)
b, Những điểm biểu diễn góc lượng giác có \(sin\left(x\right)=0,5\) là M và N.
Điểm M biểu diễn cho các góc lượng giác có số đo là \(\dfrac{\pi}{6}+k2\pi,k\in Z\)
Điểm N biểu diễn cho các góc lượng giác có số đo là \(\dfrac{5\pi}{6}+k2\pi,k\in Z\)
Trả lời bởi Hà Quang MinhXác định và so sánh tập nghiệm của các phương trình sau:
\(\begin{array}{l}a)\;x - 1 = 0\\b)\;{x^2} - 1 = 0\\c)\sqrt {2{x^2} - 1} = x\end{array}\)
\(a,x-1=0\Leftrightarrow x=1\)
Vậy tập nghiệm của phương trình là \(S=\left\{1\right\}\)
\(b,x^2-1=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là \(S=\left\{-1;1\right\}\)
c, ĐK: \(x\ge\dfrac{\sqrt{2}}{2}\)
\(\sqrt{2x^2-1}=x\Leftrightarrow2x^2-1=x^2\Leftrightarrow x^2=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là \(S=\left\{-1;1\right\}\)
Từ đó, hai phương trình b và c có cùng tập nghiệm.
Trả lời bởi Hà Quang Minh
Trong hình bên, khi bàn đạp xe đạp quay, bóng M của đầu trục quay dao động trên mặt đất quanh điểm O theo phương trình \(s = 17cos5\pi t\;\)với s (cm) là toạ độ của điểm M trên trục Ox là t (giây) là thời gian bàn đạp quay. Làm cách nào để xác định được các thời điểm mà tại đó độ dài bóng OM bằng 10cm?
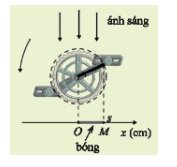
Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.
Trả lời bởi Quoc Tran Anh LeChỉ ra lỗi sai trong phép biến đổi phương trình dưới đây:
\({x^2} = 2x \Leftrightarrow \frac{{{x^2}}}{x} = 2 \Leftrightarrow x = 2\)
\(x^2=2x\)
Với x chưa khác 0 thì không thể chia (vì không có số nào chia đc cho 0)
Trả lời bởi Shinichi KudoGiải các phương trình sau:
\(\begin{array}{l}a)\;cosx = - 3\\b)\;cosx = cos{15^o}\\c)\;cos(x + \frac{\pi }{{12}}) = cos\frac{{3\pi }}{{12}}\end{array}\)
a) Với mọi \(x \in \mathbb{R}\) ta có \( - 1 \le cosx \le 1\)
Vậy phương trình \(cosx = - 3\;\) vô nghiệm.
\(\begin{array}{l}b)\,\;cosx = cos{15^o}\;\\ \Leftrightarrow \left[ \begin{array}{l}x = {15^o} + k{360^o},k \in \mathbb{Z}\\x = - {15^o} + k{360^o},k \in \mathbb{Z}\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = {15^o} + k{360^o}\) hoặc \(x = - {15^o} + k{360^o},k \in \mathbb{Z}\).
\(\begin{array}{l}c)\;\,cos(x + \frac{\pi }{{12}}) = cos\frac{{3\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{{12}} = \frac{{3\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\\x + \frac{\pi }{{12}} = - \frac{{3\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}\\x = - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = \frac{\pi }{6} + k2\pi ,\) hoặc \(x = - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
Trả lời bởi Quoc Tran Anh Le
a) Điều kiện xác định là: \(x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
Vì tan0 = 0 nên phương trình tanx = 0 có các nghiệm \(x = k\pi ,{\rm{ }}k\; \in \;\mathbb{Z}.\)
Vậy tập nghiệm của phương trình là: \(S = \{ k\pi ,{\rm{ }}k\; \in \;\mathbb{Z}\} .\)
\(\begin{array}{*{20}{l}}{b){\rm{ }}tan\left( {30^\circ -3x} \right) = tan75^\circ }\\{ \Leftrightarrow \;tan\left( {3x-30^\circ } \right) = tan\left( {-{\rm{ }}75^\circ } \right)}\\{ \Leftrightarrow \;3x-30^\circ = -75^\circ + k360^\circ ,k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;3x = -\,45^\circ + k360^\circ ,k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;x = -15^\circ + k120^\circ ,k\; \in \;\mathbb{Z}.}\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \{ -15^\circ + k120^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}\} .\)
\(\begin{array}{l}{\rm{c, cos}}\left( {x + \frac{\pi }{{12}}} \right) = {\rm{cos}}\frac{{3\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{{12}} = \frac{{3\pi }}{{12}} + k2\pi \\x + \frac{\pi }{{12}} = - \frac{{3\pi }}{{12}} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {\frac{\pi }{6} + k2\pi ; - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}} \right\}\)
Trả lời bởi Quoc Tran Anh Le