Các tứ giác trong Hình 1 có đặc điểm gì giống nhau?
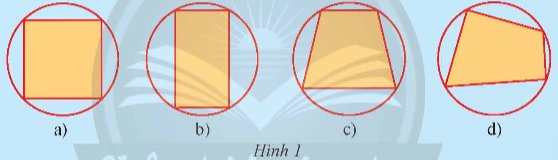
Các tứ giác trong Hình 1 có đặc điểm gì giống nhau?

Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn.
Ta có thể vẽ tứ giác nội tiếp đường tròn và một tứ giác không nội tiếp đường tròn.
Chẳng hạn:
• Tứ giác ABCD nội tiếp đường tròn (O).
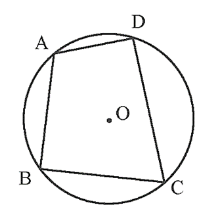
• Tứ giác A'B'C'D' không nội tiếp đường tròn (I).
Có nhận xét gì về tứ giác trong hình hoa văn trang trí mặt lưng của chiếc ghế với đường tròn trong Hình 3.

Tứ giác trong hình hoa văn trang trí mặt lưng của chiếc ghế với đường tròn trong Hình 3 là tứ giác có các đỉnh đều nằm trên đường tròn.
Trả lời bởi datcoderCho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4).
a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp \(\widehat {DAB}\) và \(\widehat {DCB}\)
b) Tính tổng số đo của các cung vừa tìm được.
c) Nêu kết luận về tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\).
d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
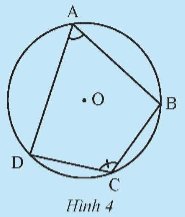
a) Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ.
Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD lớn.
b) - Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ.
Suy ra \(\widehat {DAB} = \frac{1}{2}\) số đo cung BD nhỏ.
- Góc \(\widehat {DCB}\) là góc nội tiếp chắn cung BD lớn.
Suy ra \(\widehat {DCB} = \frac{1}{2}\) số đo cung BD lớn.
Ta có \(\widehat {DAB} + \widehat {DCB} = \frac{1}{2}\) (số đo cung BD nhỏ + số đo cung BD lớn)
= \(\frac{1}{2}\).360o = 180o.
c) Tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\) bằng 180o.
d) Tổng số đo của hai góc đối diện còn lại của tứ giác ABCD là 180o
(vì 360o – 180o = 180o).
Trả lời bởi datcoderTìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6.
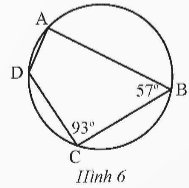
Tứ giác ABCD là tứ giác nội tiếp.
Do đó \(\widehat A + \widehat C = {180^o}\) suy ra \(\widehat A = {180^o} - \widehat C = {180^o} - {93^o} = {87^o}\).
\(\widehat B + \widehat D = {180^o}\) suy ra \(\widehat D = {180^o} - \widehat B = {180^o} - {57^o} = {123^o}\).
Trả lời bởi datcoderTrong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết \(\widehat {ABC}\) = 70o, \(\widehat {OCD}\) = 50o. Tìm góc \(\widehat {AOD}\).
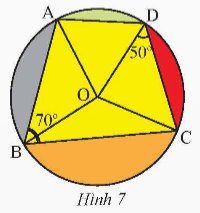
Tứ giác ABCD là tứ giác nội tiếp.
Do đó \(\widehat {ABC} + \widehat {ADC} = {180^o}\) suy ra \(\widehat {ADC} = {180^o} - \widehat {ABC} = {180^o} - {70^o} = {110^o}\).
Mà \(\widehat {ADO} + \widehat {OCD} = \widehat {ADC}\) suy ra \(\widehat {ADO} = {110^o} - {50^o} = {60^o}\).
Vì OA = OD = R nên tam giác OAD cân tại O
Suy ra \(\widehat {OAD} = \widehat {ADO} = {60^o}\) (tính chất tam giác cân)
Vậy tam giác OAD đều suy ra \(\widehat {AOD} = {60^o}\).
Trả lời bởi datcoderCho hình chữ nhật ABCD và hình vuông MNPQ (Hình 8).
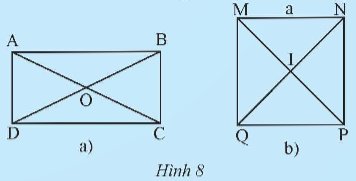
a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD.
b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
a) Độ dài các đoạn thẳng OA, OB, OC, OD là bằng nhau.
Nhận xét:
+ Tâm của đường tròn ngoại tiếp hình chữ nhật ABCD là giao điểm của hai đường chéo.
+ Đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD là đường chéo của hình chữ nhật.
b) Tâm của đường tròn ngoại tiếp hình vuông MNPQ là I.
Bán kính của đường tròn ngoại tiếp hình vuông MNPQ là:
R = IM = IN = IP = IQ = \(\sqrt {\frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{2}\).
Trả lời bởi datcoderXác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11.
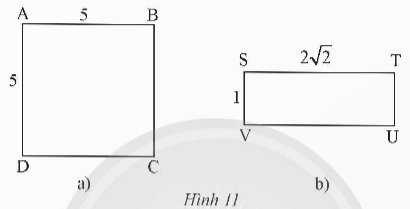
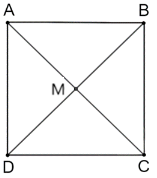
a) Hình vuông ABCD có M là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình vuông ABCD có tâm M và bán kính R = \(\frac{{a\sqrt 2 }}{2} = \frac{{5\sqrt 2 }}{2}\).
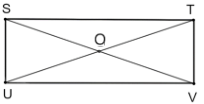
b) Hình chữ nhật STUV có O là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình chữ nhật STUV có tâm O và bán kính
R = \(\frac{{SU}}{2} = \frac{{\sqrt {S{T^2} + U{T^2}} }}{2} = \frac{{\sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {1^2}} }}{2} = \frac{{\sqrt 9 }}{2} = \frac{3}{2}\).
Trả lời bởi datcoderMột người muốn thiết kế một bảng hiệu gồm một hình vuông nội tiếp một đường tròn bán kính R = 3 cm (Hình 12). Tính diện tích hình vuông đó.

Ta thấy đường tròn ngoại tiếp hình vuông suy ra độ dài đường chéo hình vuông là đường kính của hình tròn.
Độ dài của đường chéo hình vuông là: d = 2.R = 2.3 = 6 cm.
Độ dài cạnh hình vuông là: a = \(\sqrt {\frac{{{d^2}}}{2}} = \sqrt {\frac{{{6^2}}}{2}} = 3\sqrt 2 \) cm.
Diện tích hình vuông là: \(3\sqrt 2 .3\sqrt 2 \) = 18 (cm2).
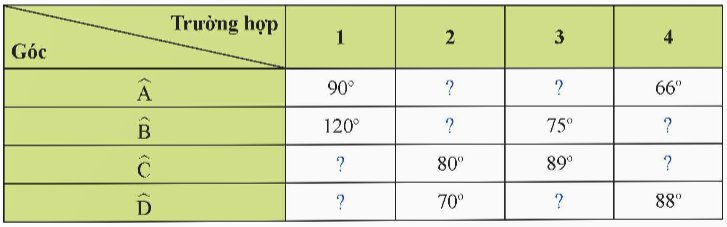
Trả lời bởi datcoderCho ABCD là tứ giác nội tiếp. Hãy hoàn thành bảng sau vào vở.
Các tứ giác trong Hình 1 đều có các đỉnh nằm trên đường tròn.
Trả lời bởi datcoder