Cho tứ diện ABCD. Gọi P, Q, R và S là bốn điểm lần lượt lấy trên 4 cạnh AB, BC, CD và DA. Chứng minh rằng nếu 4 điểm P, Q, R và S đồng phẳng thì :
a) Ba đường thẳng PQ, SR và AC hoặc song song hoặc đồng quy
b) Ba đường thẳng PS, RQ và BD hoặc song song hoặc đồng quy
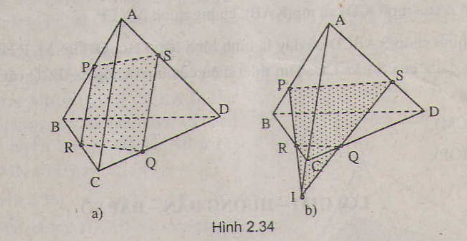







a) Gọi mặt phẳng qua bốn điểm P, Q, R, S là (α). Ba mặt phẳng ( α), (ABC) và (ACD) đôi một cắt nhau theo các giao tuyến là PQ, AC, RS => PQ, AC, RS hoặc đôi một song song hoặc đồng quy
b) Chứng minh tương tự ta được ba đường thẳng PS, RQ, và BD hoặc song song hoặc đồng quy
Trả lời bởi qwerty