Có 10 đội tham gia một giải bóng đá. Có bao nhiêu cách xếp trận đấu vòng tính điểm sao cho hai đội chỉ gặp nhau đúng một lần?
$3. Tổ hợp
QL
Hướng dẫn giải
Thảo luận (1)
QL
Khối 10 có 16 bạn nữ và 18 bạn nam tham gia đợt tình nguyện Mùa hè xanh. Đoàn trường dự định lập một tổ trồng cây gồm 3 học sinh có cả nam và nữ. Có bao nhiêu cách lập một tổ trồng cây như vậy?
Hướng dẫn giải
Thảo luận (1)
+) Số cách chọn 3hs bất kì trong 34hs là: \(C_{34}^3\) ( cách chọn)
+) Số cách chọn 3hs nam trong 34hs là: \(C_{18}^3\) ( cách chọn)
+) Số cách chọn 3hs nữ trong 34hs là: \(C_{16}^3\) ( cách chọn)
+) Số cách chọn 3hs gồm cả nam và nữ trong 34hs là: \(C_{34}^3 - C_{18}^3 - C_{16}^3 = 4608\) ( cách chọn)
Trả lời bởi Hà Quang Minh
QL
Trong một buổi tập huấn cho các bí thư chi đoàn có 10 bạn nam. Hỏi có bao nhiều cách chọn 3 bạn nam để tham gia một trò chơi?
Hướng dẫn giải
Thảo luận (1)
Mỗi cách chọn 3 bạn nam trong 10 bạn nam là một tổ hợp chập 3 của 10 phần tử.
Do đó có \(C_{10}^3 = 120\) (cách chọn)
Trả lời bởi Hà Quang Minh
QL
Cho 8 điểm sao cho không có 3 điểm nào thẳng hàng. Có bao nhiêu tam giác với 3 đỉnh là 3 điểm trong 8 điểm đã cho?
Hướng dẫn giải
Thảo luận (1)
Số tam giác với 3 đỉnh là 3 điểm trong 8 điểm đã cho là tổ hợp chập 3 của 8 phần tử, do đó số tam giác là: \(C_8^3\) ( tam giác)
Trả lời bởi Hà Quang Minh
QL
Dùng máy tính cầm tay để tính:
a)\(C_{25}^{13}\)
b)\(C_{30}^{25}\)
Hướng dẫn giải
Thảo luận (1)
QL
Cho tập hợp A = {a, b, c, d, e}.
a) Nêu cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
b) Nêu cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A.
c) So sánh cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A với cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
Hướng dẫn giải
Thảo luận (1)
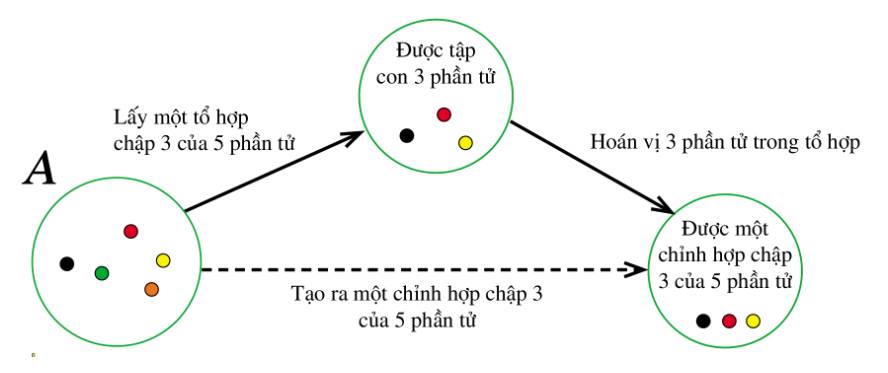
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh: Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.
QL
Đội tuyển bóng bàn nam của trường có 4 bạn Mạnh, Phong, Cường, Tiến. Huấn luyện viên muốn chọn 2 bạn để tạo thành một cặp đấu đôi nam.
a) Nêu 3 cách chọn cặp đấu.
b) Mỗi cặp đấu là một tập con gồm bao nhiêu phần tử được lấy ra từ tập hợp gồm 4 bạn nói trên?
Hướng dẫn giải
Thảo luận (1)
a) Ba cách chọn cặp đấu sẽ là:
+) Cách 1: Chọn Mạnh và Phong
+) Cách 2: Chọn Cường và Tiến
+) Cách 3: Chọn Phong và Cường
b) Mỗi cặp đấu gồm có 2 người nên mỗi cặp đấu là một tập con gồm 2 phần tử được lấy ra từ tập hợp gồm 4 bạn nói trên.
Trả lời bởi Hà Quang Minh
QL
Trong một giải bóng bàn đôi nam, mỗi đội 8 người chọn 2 vận động viên để tạo thành một cặp đấu.

Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là gì?
Hướng dẫn giải
Thảo luận (1)
Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là một tổ hợp chập 2 của 8.
Trả lời bởi Hà Quang Minh
QL
Viết tất cả tổ hợp chập 2 của 3 phần tử a, b, c.
Hướng dẫn giải
Thảo luận (1)
Tất cả các tổ hợp chập 2 của 3 phần tử a,b,c là các tập con gồm 2 phần tử được lấy ra từ tập hợp gồm 3 phần từ a,b,c là: \(\left\{ {a;b} \right\},\left\{ {a;c} \right\},\left\{ {b;c} \right\}\)
Trả lời bởi Hà Quang Minh
QL
So sánh:
a) \(C_6^2\) và \(C_6^4\)
b) \(C_4^2 + C_4^3\) và \(C_5^3\)
Hướng dẫn giải
Thảo luận (1)
a) Sử dụng máy tính cầm tay, ta có:
\(\left. \begin{array}{l}C_6^2 = 15\\C_6^4 = 15\end{array} \right\} \Rightarrow C_6^2 = C_6^4\)
b) Sử dụng máy tính cầm tay, ta có:
\(\left. \begin{array}{l}C_4^2 + C_4^3 = 6 + 4 = 10\\C_5^3 = 10\end{array} \right\} \Rightarrow C_4^2 + C_4^3 = C_5^3\)
Trả lời bởi Hà Quang Minh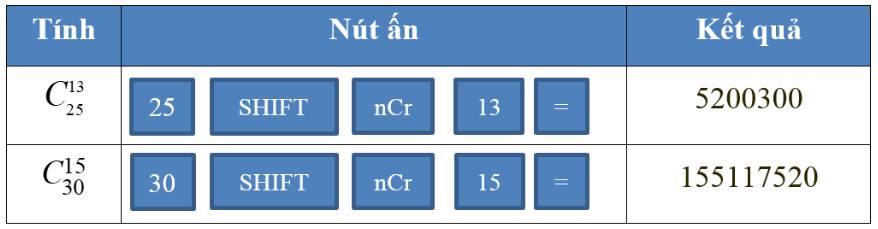
Số cách xếp trận đấu vòng tính điểm để cho hai đội chỉ gặp nhau đúng một lần là tổ hợp chập 2 của 10 phần tử, do đó số cách xếp trận đấu là: \(C_{10}^2 = 45\) (cách xếp)
Trả lời bởi Hà Quang Minh